11.4. Naturaleza de la luz
Al terminar el siglo XX nos encontramos en un mundo en el cual la tecnología ha tenido
un desarrollo tan prodigioso que ya nada parece imposible de conseguir.
Este enorme desarrollo podría hacernos creer que el pasado siglo XX ha sido el siglo de
la Ciencia, pero no debemos engañarnos, pues la mayor parte de este progreso ha tenido
su origen en el siglo XIX. Recordemos el origen de los automóviles, de la aviación, de los
viajes espaciales, de la radio, de la televisión, de la cibernética, etc.
Y podremos comprobar que los principios físicos de estas realizaciones ya eran conocidos
en aquel tiempo.
A lo largo de la historia se han producido grandes descubrimientos en el campo de la
Física, pero al mismo tiempo se han planteado muchas preguntas que han quedado sin
responder. Hagamos un breve repaso de la situación actual de los conocimientos que
tenemos sobre los fenómenos de la Naturaleza:
Conocemos la ley que rige las fuerzas gravitatorias, pero no tenemos una explicación
concreta de estas fuerzas que actúan a distancia.
Se han determinado las leyes que rigen los campos de fuerza eléctricos, pero tampoco se
puede explicar cómo se extienden en el espacio.
Se conoce la relación que existe entre el movimiento de las cargas eléctricas y la fuerza
magnética que se produce, pero se ignora por qué se produce esta fuerza.
Se sabe que una variación de flujo magnético genera un campo eléctrico, pero no hay
explicación para este fenómeno.
Hablamos de ondas electromagnéticas, pero ignoramos su naturaleza concreta, y además
ignoramos si todas las radiaciones son de la misma naturaleza.
Actualmente no existe una teoría suficientemente razonada que explique cómo se
mantienen unidos los protones que constituyen un núcleo atómico, cuando teniendo una
fuerte carga eléctrica positiva deberían ser fuertemente repelidos entre sí. Por ello ha sido
necesario invocar una extraña fuerza llamada “fuerza nuclear intensa” cuyas leyes no se
han podido determinar.
La física moderna se ve obligada a crear una variedad de conceptos poco inteligibles,
para explicar los resultados de algunos experimentos que le proporciona una tecnología
muy avanzada, porque carece todavía de unos principios básicos en los cuales pueda
apoyar una explicación suficientemente razonada.
En el transcurso del siglo XX, algunos científicos, entre ellos el propio Einstein, han
tratado de encontrar una teoría unificada que relacione entre sí el campo gravitatorio, el
campo eléctrico y el campo magnético, pero a pesar del gran interés puesto en esta
empresa, ninguna teoría ha sido establecida hasta ahora.
Esta situación de estancamiento en los principios fundamentales de la Física nos debería
obligar a pensar que en las Teorías de Einstein o en las teorías clásicas puede haber algo
que no sea correcto y ser la causa de este bloqueo.
En la actualidad es tan grande la cantidad de conocimientos adquiridos, que los científicos
no tienen más recurso que especializarse en alguna de las materias para poder afrontar la
situación, pero esta especialización no es buena para desentrañar los principios más
profundos de la Física y menos si pretendemos establecer una teoría unificada, puesto
que tendremos que trabajar en numerosos campos para encontrar la convergencia de
todas las leyes físicas en algún punto desconocido.
Aquellos que conocen los principios en que se basa el funcionamiento de un moderno
ordenador, capaz de realizar funciones de gran complejidad saben que todo el proceso se
basa en una cosa tan simple como “sí o no”. Un sistema binario.
Pues bien, en los principios fundamentales de la Física habremos de encontrar algo
parecido ¿pero cómo llegar a ello?
Un buen criterio científico no debe considerar como definitiva ninguna explicación de un
fenómeno físico, ni tampoco descartar para siempre algunas ideas que se rechazaron en
un momento determinado porque no encajaban bien con los conceptos que prevalecían
en aquel tiempo.
En opinión del autor, la Física actual sigue un camino que empezó a desviarse de la
dirección correcta a partir del experimento famoso de Michelson-Morley realizado en el
año 1881, que se interpretó incorrectamente y que después se reafirmó con la Relatividad
Especial de Einstein. En ambos casos se descartó la existencia del éter, lo cual originó
una gran confusión entre los científicos de la época, quienes creían que ya casi conocían
todas las leyes de la Física.
No deberíamos tener miedo a efectuar una revisión de los principios establecidos para
corregir todos aquellos que sea necesario, siempre que la corrección sea razonable y
coherente con todos aquellos principios que no ofrecen ninguna duda.
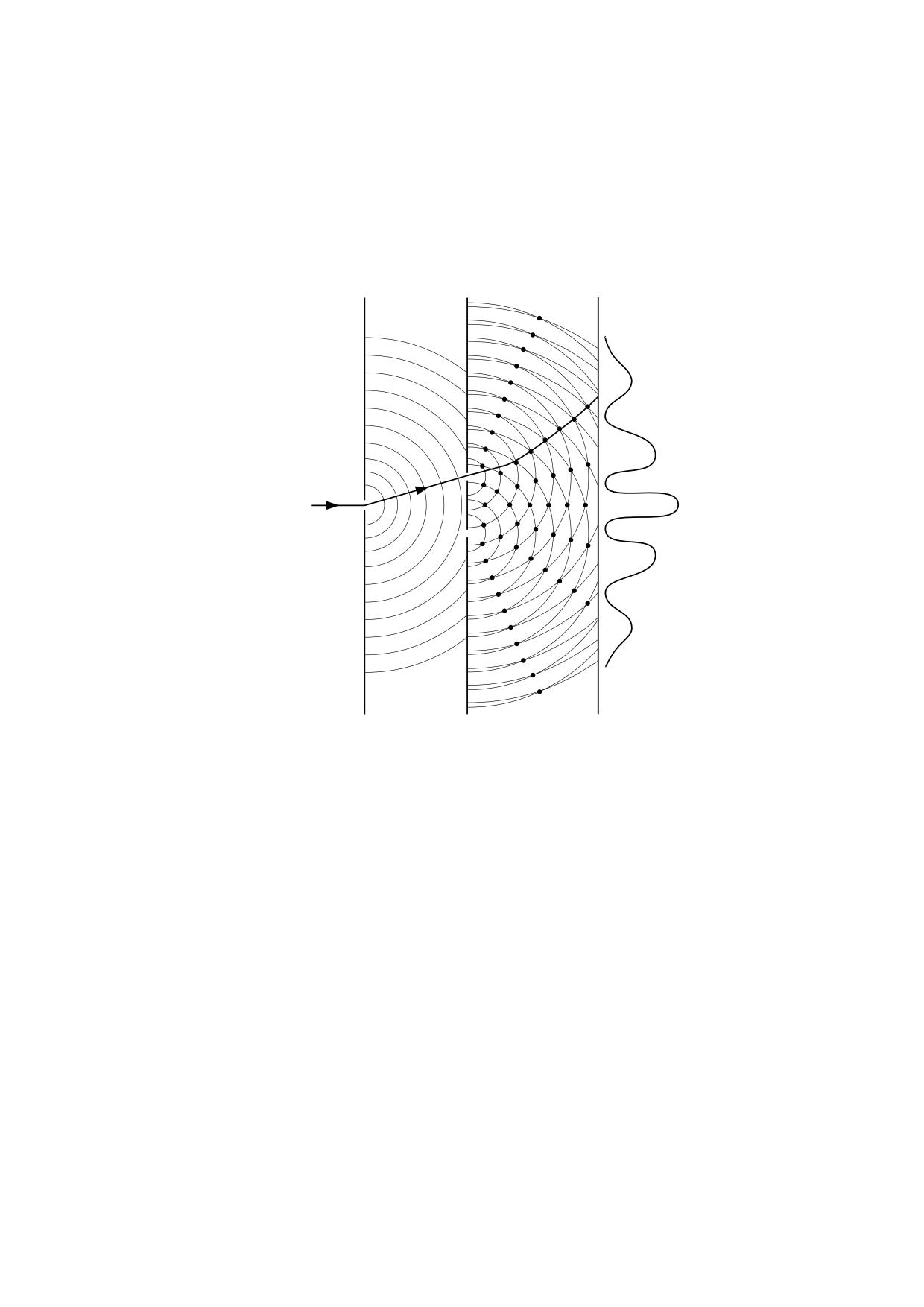
En la época en que se realizó el experimento de Michelson se tenía la creencia de que la
luz era un fenómeno puramente ondulatorio, que se producía en el éter y que este se
mantenía fijo en el espacio, de modo que la Tierra se desplazaba a través del mismo.
Michelson tuvo conocimiento de que Maxwell había concebido la posibilidad de detectar el
desplazamiento del sistema solar respecto al éter fijo, lo que le indujo a inventar un
ingenioso procedimiento basado en la interferencia de un rayo de luz propagándose en la
dirección del movimiento de la tierra, con otro rayo de luz coherente dirigido
perpendicularmente al anterior, con lo cual se conseguía una precisión extraordinaria.
El resultado de este experimento y de otros que le siguieron fue decepcionante, pues a
pesar de su gran precisión no acusó ningún movimiento relativo entre la tierra y el éter fijo.
Por otro lado, si se consideraba que el éter era arrastrado por la tierra acompañándola en
su movimiento, para justificar los resultados, entraba entonces en contradicción con el
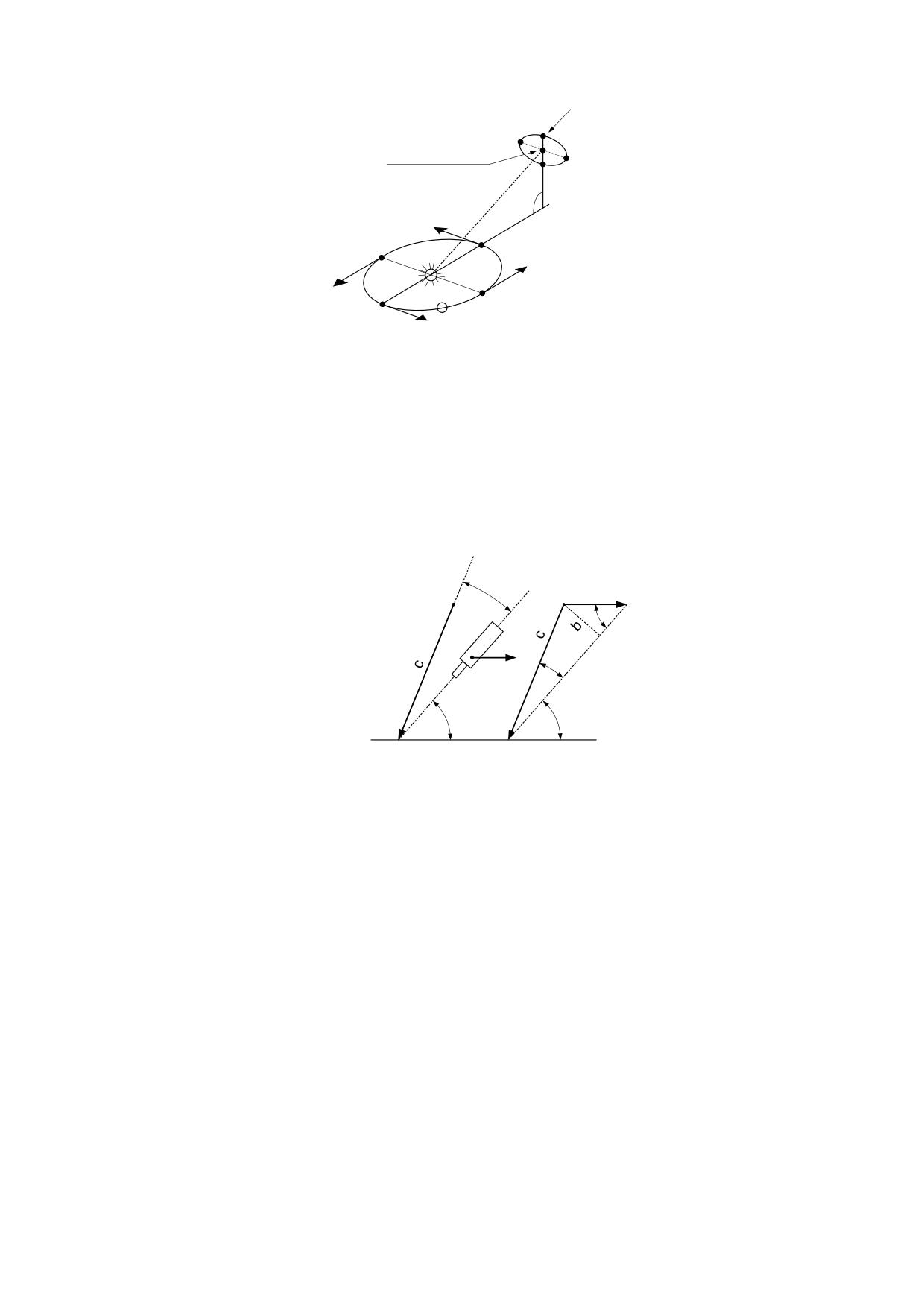
fenómeno de la aberración de la luz de las estrellas, descubierto por el astrónomo inglés
Bradley en el año 1725 y que tenía su explicación de acuerdo con las leyes de la
propagación ondulatoria basada sobre el principio de Huygens.
Este fracaso desorientó a los científicos de aquella época, lo que dio lugar a que se
rechazase el éter como el medio de propagación de las ondas electromagnéticas y se
concibió la idea de la propagación en el vacío.
Este experimento no hubiera fracasado si se hubiera considerado que el éter, como
cualquier materia sigue las leyes de la gravitación y por lo tanto acompaña a la tierra y
gira con ella, pero también era necesario renunciar a la trayectoria ondulatoria de la luz y
admitir la teoría corpuscular que postula trayectorias balísticas, pero sin renunciar al
comportamiento ondulatorio que demuestran los fenómenos de interferencia. En el fondo
del problema estaba el extraño comportamiento de la luz, que unas veces aparenta ser un
fenómeno ondulatorio mientras en otros casos se comporta como un movimiento de
partículas.
Lo expuesto anteriormente nos lleva a preguntar:
¿Es realmente la luz una radiación electromagnética pura?
¿Tienen la misma naturaleza las ondas radioeléctricas y la luz?
Fue Einstein quien demostró la naturaleza cuántica de la luz, y que después confirmó
Milikan, creando el concepto del fotón, pero ni ellos ni nadie hasta ahora ha podido hacer
una descripción del mismo. Es un concepto tan ambiguo que hasta acepta que una onda
de radio con longitud de onda de 1 Km. esté constituida por fotones, lo cual resulta
bastante difícil de aceptar.
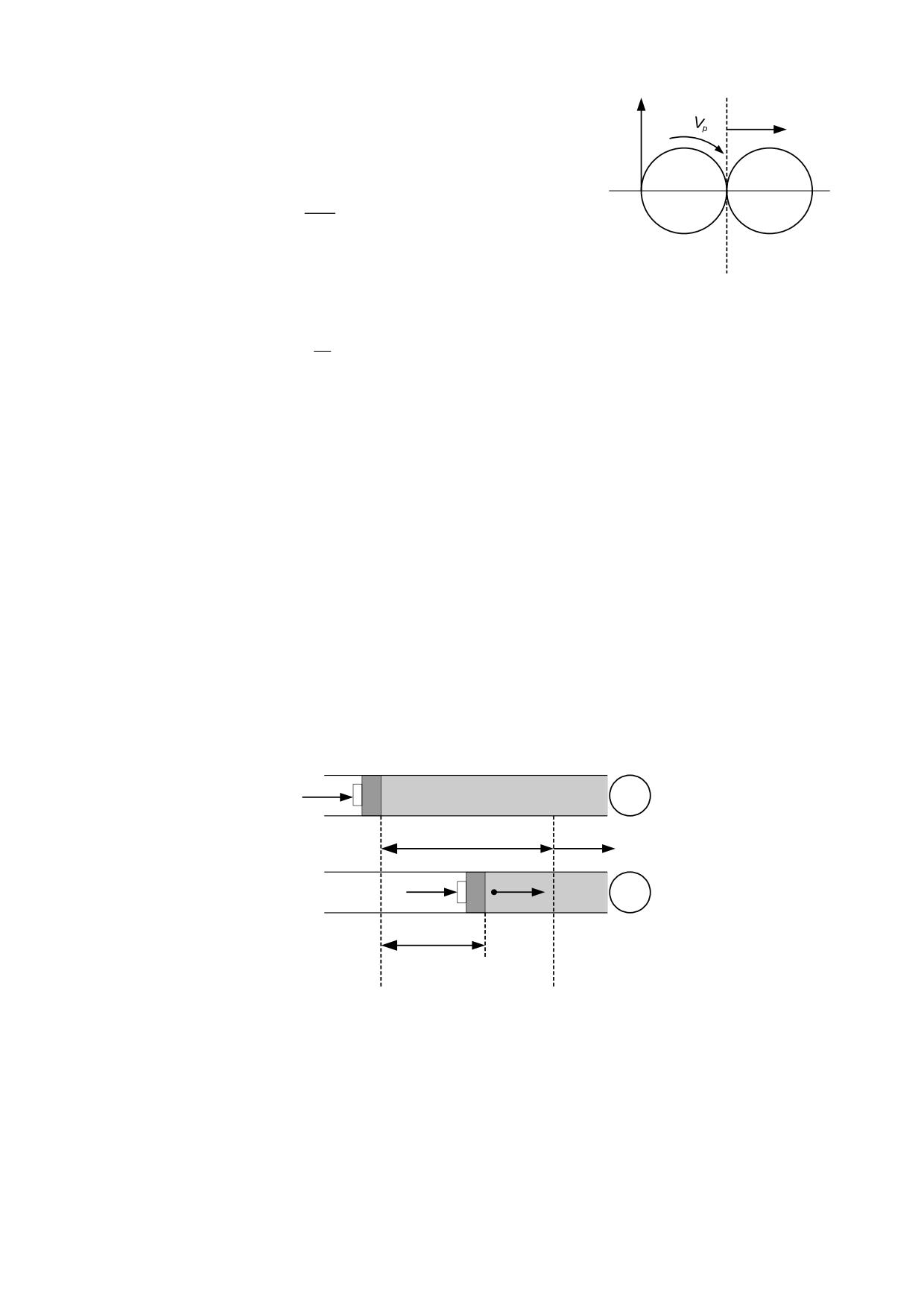
Para justificar el resultado del experimento de Michelson podemos anticipar un nuevo
concepto de los fotones, que será desarrollado en el capítulo que trata de la luz : los
fotones son un conjunto de partículas con masa y carga eléctrica equilibrada, dispuestas
de tal modo que al avanzar a través del éter originan en éste una onda electromagnética
transversal que los acompaña en su desplazamiento, siguiendo una trayectoria balística
debido a la inercia de la masa que transportan. La onda asociada es la responsable de los
fenómenos de interferencia que se producen al superponerse dos rayos de luz.
El autor de este trabajo ha desarrollado una teoría con un nuevo concepto del éter que
consigue la unificación de todos los campos de fuerza, pero la mera concepción de un
nuevo modelo de éter no habría sido suficiente por sí misma para conseguir una teoría
unificada, pues el autor ha encontrado que tanto en la Electrodinámica Clásica como en la
Relatividad Especial había algunos postulados que parecían falsos y era necesario
corregirlos. Esto resultó una tarea ardua, pero finalmente fue posible conseguir que todo
resultase coherente.
Es frecuente encontrar personas que piensan que el concepto de relatividad ha sido una
creación de Einstein, cuando la verdad es que la relatividad del movimiento ya fue
descubierta por Galileo y plenamente asumida por Newton.
Lo que Einstein realmente propuso fue la “Relatividad Especial” en la cual se imponen
algunas restricciones al concepto que tenían Galileo y Newton sobre la relatividad.
Posteriormente Einstein desarrolló su “Relatividad General” para poder explicar ciertos
fenómenos observados en el firmamento, tales como la curvatura de los rayos de la luz en
las proximidades de los astros debido al campo gravitatorio, el corrimiento del espectro de
frecuencias de la luz de las estrellas, etc.
Los resultados de esta última teoría son satisfactorios en cuanto sirven para calcular la
magnitud de los fenómenos mencionados, así como para corregir trayectorias de naves
espaciales, pero la gran complicación matemática de esta teoría resulta difícil de entender
y además sus principios no son convincentes.
En el año 1920 Einstein presentó un informe en la universidad de Leyden titulado “Ether
and the theory of relativity” que contiene argumentos de mucho interés a favor del éter y
que sin embargo son poco conocidos, además de estar en contradicción con la
“Relatividad Especial” que él mismo había establecido.
Este informe termina con la siguiente conclusión que traducimos así: “Recapitulando,
podemos decir que de acuerdo con la relatividad el espacio está dotado con propiedades
físicas; en este sentido, por consiguiente, existe algún éter. De acuerdo con la teoría de la
relatividad general el espacio sin éter es impensable; pues en tal espacio no solo no
habría propagación de la luz, sino también imposibilidad de medidas de espacio y tiempo,
ni por lo tanto cualquier intervalo espacio-tiempo en el sentido físico”.
2.1. El éter tiene existencia real
En principio se pensaba que las fuerzas gravitatorias, eléctricas y magnéticas, se ejercían
a distancia a través del vacío o de algún medio que ocupaba el vacío. Más tarde la
experimentación con las ondas electromagnéticas demostraba que una fuerza ejercida
sobre un cuerpo no requiere la presencia de aquel otro cuerpo que dio origen a dicha
fuerza. Esto obliga a aceptar la idea de que un cuerpo puede alterar el espacio
circundante de distintos modos, dependiendo de su masa, de su carga eléctrica y de su
movimiento. Esta alteración se propaga en el espacio y ejerce su efecto sobre otros
cuerpos situados a distancia.
Ya no es correcto pensar que un cuerpo ejerce una fuerza sobre otros cuerpos situados a
distancia. Deberemos asumir que un cuerpo altera de algún modo el espacio inmediato y
que esta alteración se propaga en el espacio con determinada velocidad, provocando
algún tipo de fuerza sobre los cuerpos situados en la región afectada.
Pero el vacío absoluto solo se puede alterar ocupándolo con algo, pues la nada no se
puede cambiar sin dejar de ser la nada y entonces nos preguntamos: ¿qué cosa es la que
ocupa el espacio vacío?
Los fenómenos electromagnéticos demuestran que es necesaria la presencia de un medio
de referencia como veremos a continuación :
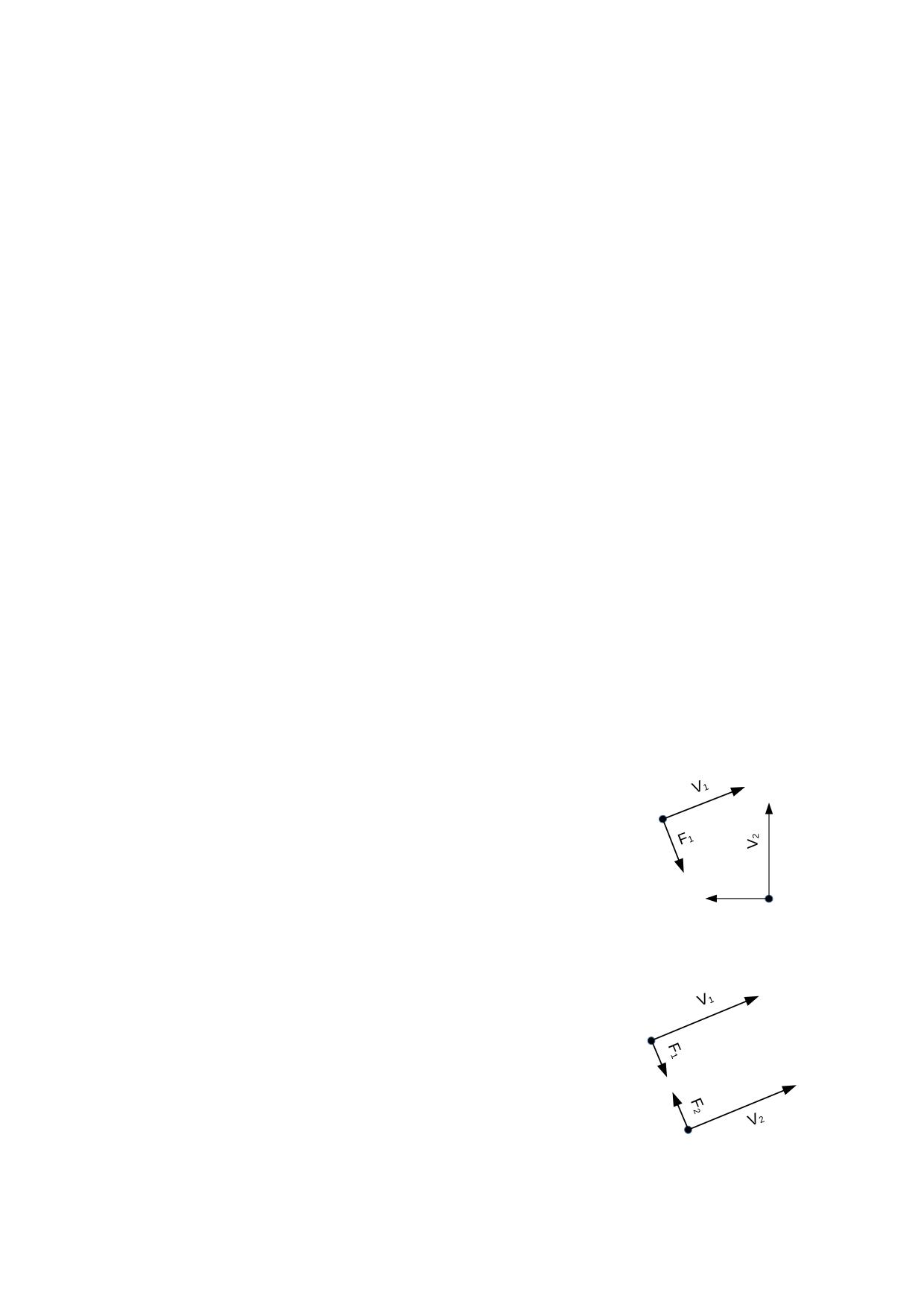
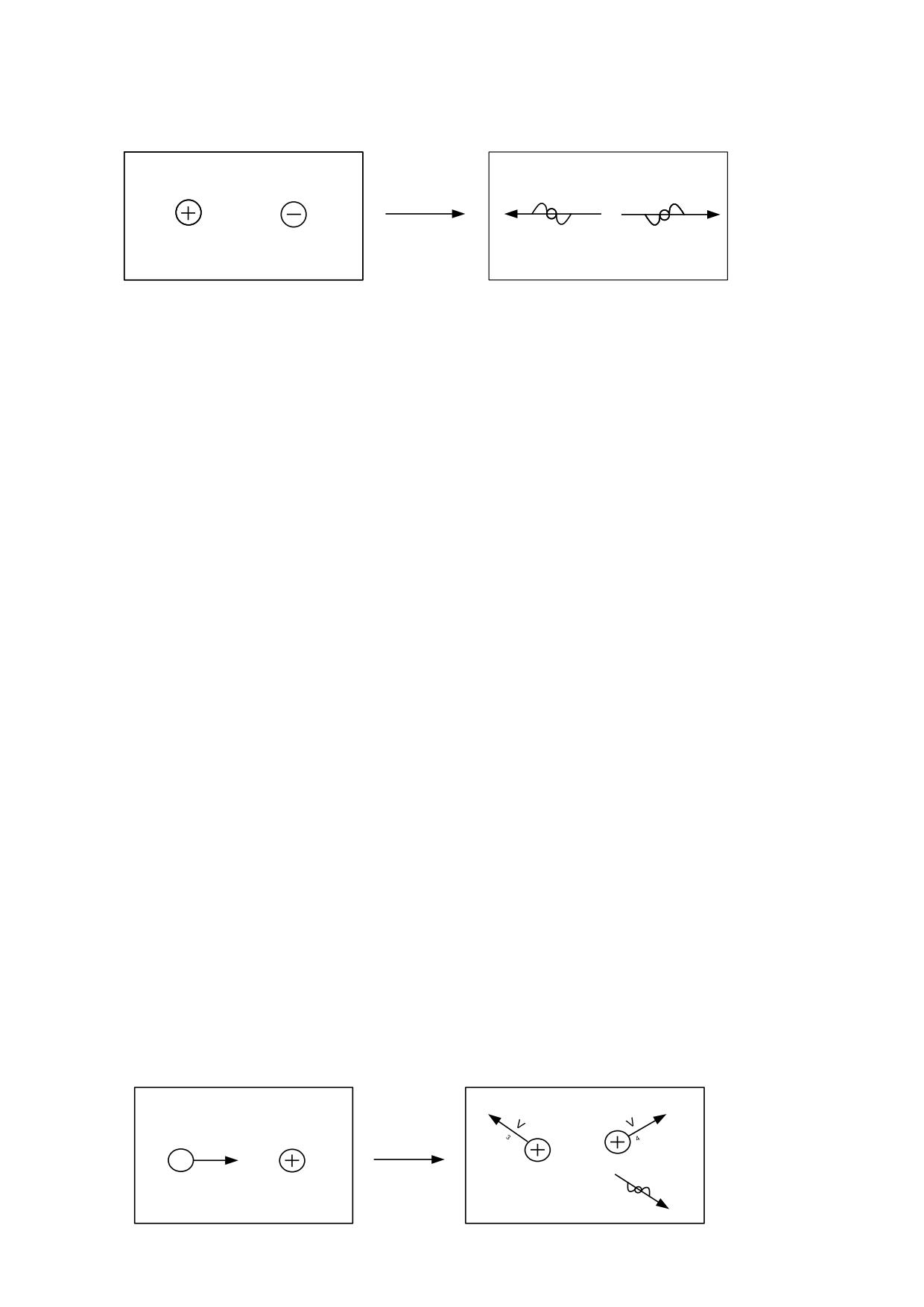
Sabemos que cuando una carga eléctrica se desplaza en las proximidades de otra carga
que también se mueve, además de la fuerza eléctrica, se produce otra fuerza magnética
con sentido perpendicular al movimiento, de acuerdo con la fig. 2.1.1 donde solo se
representan las fuerzas magnéticas.
Podemos observar que no se cumple entre dichas cargas
el principio de acción y reacción propuesto por Newton.
+q1
Si ahora dejamos una de las dos cargas en reposo y
movemos la otra con un movimiento relativo equivalente,
comprobaremos que no se produce ninguna fuerza
F2
+q2
magnética.
fig. 2.1.1
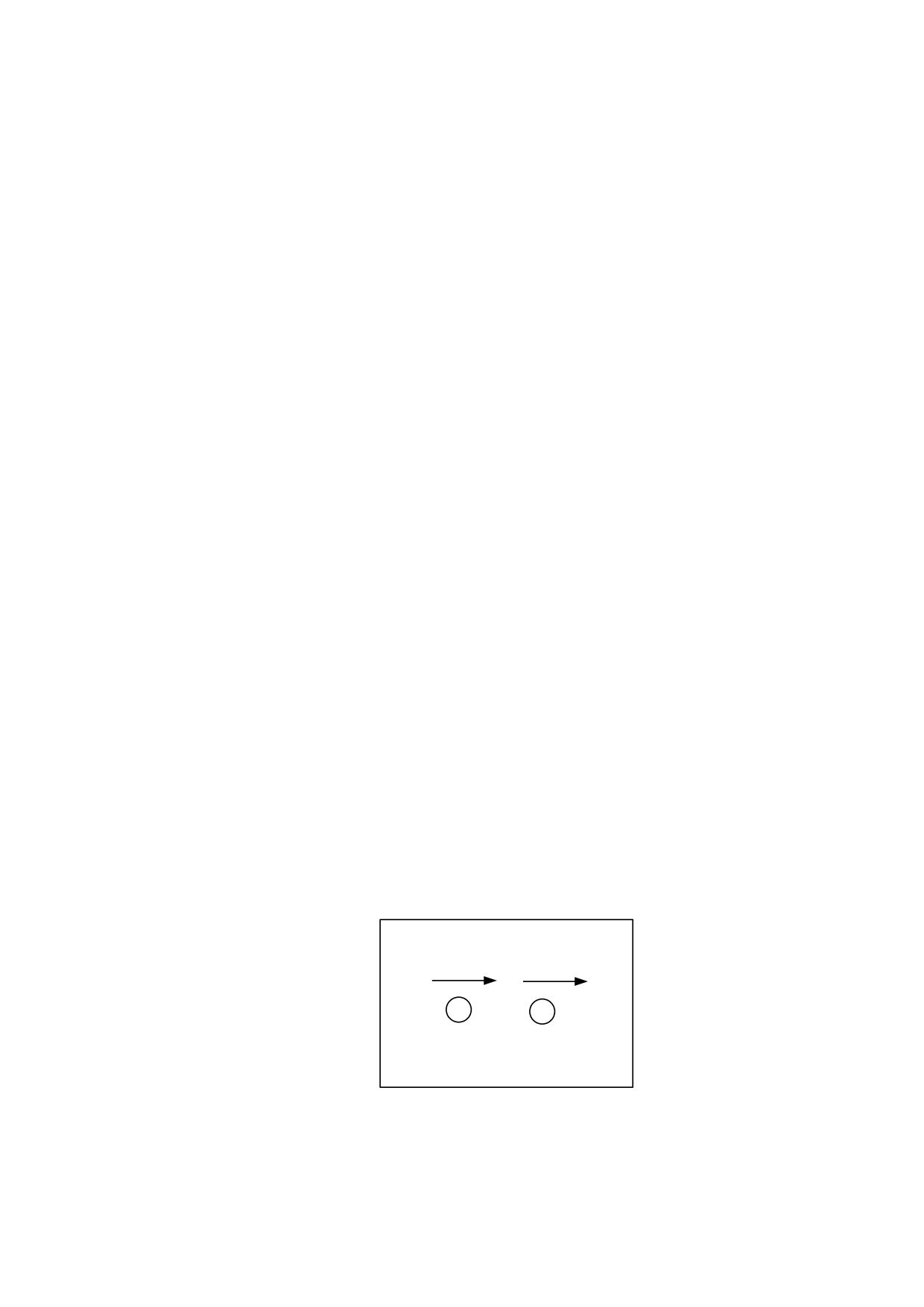
Por el contrario dos cargas que se mueven en la misma
dirección y sentido, con la misma velocidad, sufren una
fuerza magnética perpendicular a la dirección del
movimiento, aunque el movimiento relativo entre ellas sea
+q1
V1=V2
nulo, según se representa en la fig. 2.1.2.
Este comportamiento demuestra sin ninguna duda que no
es el movimiento relativo entre las dos cargas eléctricas el
causante de la fuerza magnética, sino el movimiento de
+q2
las cargas respecto a un medio de referencia que debe
fig. 2.1.2
estar en reposo respecto a nuestro laboratorio.
Todo lo expuesto anteriormente nos obliga a pensar que para que se produzcan los
fenómenos electromagnéticos es necesario un marco de referencia que al mismo tiempo
sea el medio de propagación de los campos de fuerza electromagnética.
Este medio de propagación es el éter, pero no un éter fijo en el espacio, como se pensaba
en el siglo XIX, sino un éter que acompaña a la Tierra en sus movimientos y que está
distribuido en el universo de acuerdo con las leyes gravitatorias, como corresponde a un
ente material.
La presencia del éter que nos ha permitido la explicación de los fenómenos expuestos
anteriormente, además justifica el cumplimiento del principio de acción y reacción, porque
esta reacción se produce sobre el propio éter como intermediario que es. Sería imposible
sostener el principio de Newton apoyándose en el vacío absoluto, pero también sería
difícil el rechazar este principio, porque se cumple siempre en los fenómenos que son
bien conocidos.
2.2. Descripción del éter
Debido a que el éter es una materia intangible no podemos determinar sus propiedades
de una manera directa y por lo tanto nos vemos obligados a deducir sus características
basándonos en los efectos que produce su presencia, limitándonos a definir aquellas
propiedades que se consideran necesarias para cumplir la función que le corresponde en
determinados fenómenos, hasta que futuras experiencias nos proporcionen un
conocimiento más profundo del mismo.
Una propiedad que debe tener el éter es la de comportarse como un cuerpo dieléctrico,
con una constante dieléctrica igual a la que actualmente se adjudica al vacío.
Deberá tener una fluidez tal que le permita ocupar los espacios libres existentes entre las
partículas subatómicas.
Como toda la materia, deberá estar constituido por cargas eléctricas positivas y negativas.
Deberá tener masa y consecuentemente inercia.
Deberá ser elástico, lo que determinará que su densidad sea variable en función de la
presión.
Su estructura debe permitir que sus elementos puedan girar sin producir rozamiento.
Esta última característica no se encuentra en la materia ordinaria y parece una condición
inalcanzable, pero el éter la posee gracias a una estructura especial, la cual vamos a
deducir basándonos en fenómenos bien conocidos.
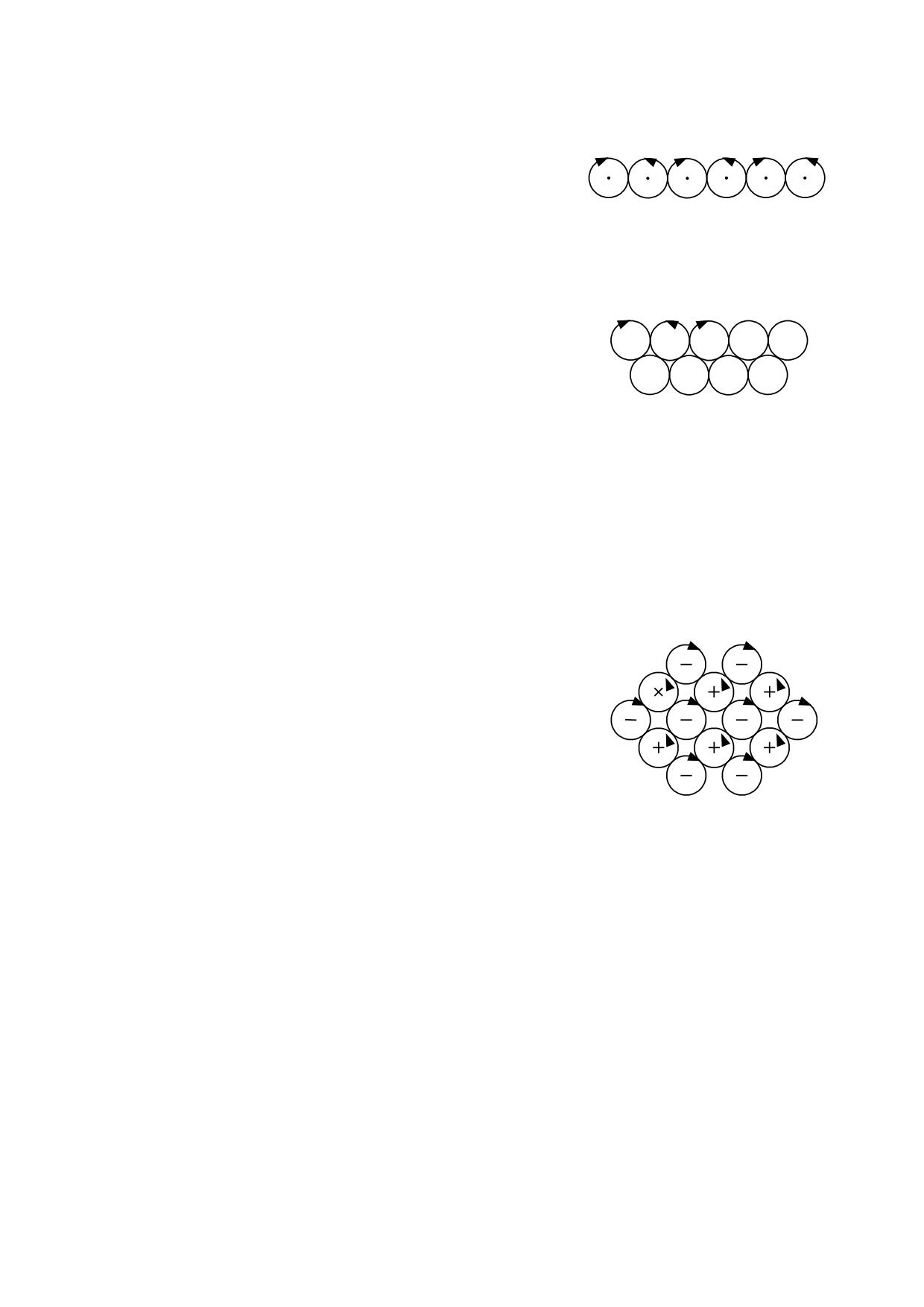
Si intentamos construir con materia ordinaria un conjunto
de elementos rotatorios que se mantengan en contacto y
que puedan girar con rodadura perfecta, encontraremos
que una sola configuración es posible; aquella que tiene
fig. 2.2.1
sus elementos ordenados en una fila única, en la cual los
elementos que tienen contacto giran en sentidos
contrarios, como muestra la fig. 2.2.1.
Pero si llenamos cualquier volumen con elementos que
tomen contacto entre sí, encontraremos que no pueden
girar porque resultan aplicadas sobre un mismo elemento
?
fuerzas de sentido contrario, tal como se demuestra en la
fig. 2.2.2
fig. 2.2.2 que tiene más de una fila.
Sin embargo conocemos ciertas propiedades de la materia que nos van a proporcionar
una solución muy sencilla.
Sabemos que en la constitución de la materia participan las cargas eléctricas de ambos
signos y también conocemos que el movimiento de las cargas eléctricas genera el campo
magnético.
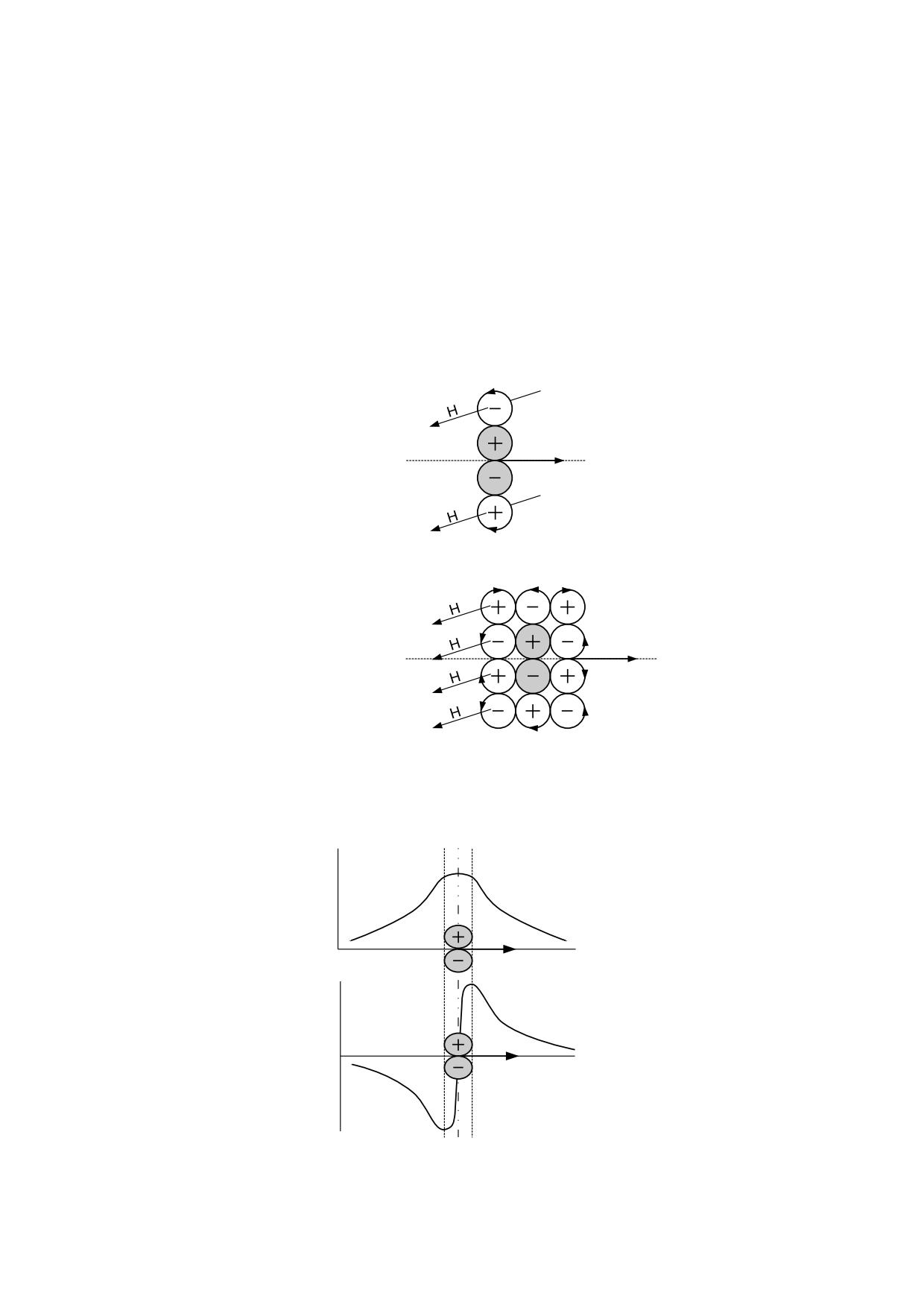
Imaginemos un gran número de partículas esféricas, unas
con carga eléctrica positiva y otras con carga negativa,
que dejamos en libertad para que se agrupen de acuerdo
con el signo de su carga. Las cargas de distinto signo
tenderán a juntarse, al mismo tiempo que desplazarán a
las de su mismo signo, hasta alcanzar una distribución
que consiga el equilibrio del conjunto.
Solamente quedarán en contacto las cargas de signo
opuesto, mientras quedarán separadas las cargas del
fig. 2.2.3
mismo signo, según muestra la Fig. 2.2.3.
Esta configuración permitirá una rodadura perfecta y además proporciona el fundamento
de un campo magnético, debido a que todas las cargas del mismo signo giran en el
mismo sentido mientras las de signo contrario giran en sentido opuesto, lo cual es la
condición necesaria para sustentar un campo magnético de sentido único.
Hasta aquí hemos considerado únicamente la distribución de los elementos sobre un
plano, pero aplicando los mismos principios para una distribución en tres dimensiones
encontraremos que resulta una estructura en red cúbica, como queda representada en la
fig. 2.2.4.
A las partículas que constituyen el éter las denominaremos en adelante “eterones” con el
fin de facilitar el lenguaje.
No deberemos pensar que el éter es un gas sutilísimo, como siempre se ha creído, pues
realmente su naturaleza se parece más a un cristal, a pesar de que sea el mismo un fluido
y tenga la propiedad de su compresibilidad.
Es conveniente resaltar la diferencia esencial que existe
entre el éter y lo que consideramos materia ordinaria:
sabemos que la materia está constituida por átomos y
estos a su vez se componen de partículas que tienen una
gran densidad de masa y que están separadas entre sí
por distancias relativas enormes. Dicho de otro modo: la
materia ordinaria está estructurada de manera
discontinua, comparable a la de nuestro sistema solar,
mientras que el éter debe tener una estructura continua,
fig. 2.2.4
sin separación entre sus componentes los eterones.
El tamaño de los eterones debe ser muy pequeño en relación con las partículas
subatómicas, pero en la actualidad no se puede hacer ninguna estimación porque
carecemos de cualquier referencia.
Los eterones se caracterizan por la propiedad de ser elásticos, lo que implica que la
densidad de carga en un sector puede variar bajo el efecto de una presión ejercida en un
punto, que al mismo tiempo deformará la superficie esférica.
Esta característica permite también que el contacto con una carga eléctrica de signo
opuesto origine un aumento de densidad de carga en la zona de contacto, lo cual equivale
a un desplazamiento de la carga del eterón.
2.3. Fuerza coeléctrica y fuerzas inducidas.
La física clásica ha creado el concepto de campo de fuerza para explicar los fenómenos
de fuerzas ejercidas a distancia. Este es un concepto abstracto que ha permitido
establecer diversas leyes que permiten hacer cálculos sobre estos fenómenos, pero sobre
los cuales no hay hasta ahora una explicación concreta. Tampoco ha sido posible
encontrar la relación que existe entre los distintos campos de fuerza.
En esta Física del Éter se demuestra que las fuerzas no se ejercen a distancia en el
vacío, sino que las fuerzas se ejercen siempre por el contacto directo de los elementos,
siendo el éter el elemento que permite que estas fuerzas se manifiesten aparentemente a
distancia. Son los distintos modos de alteración del éter lo que produce los diferentes
campos de fuerza, ya sean campos gravitatorios, eléctricos o magnéticos.
El origen de todas las fuerzas reside en las cargas eléctricas elementales que constituyen
toda la materia, incluido el éter. Sabemos que las cargas eléctricas de distinto signo se
atraen y que las del mismo signo se repelen. (Más adelante demostraremos que esto solo
es cierto cuando se interpone el éter entre las cargas eléctricas).
Antes de pasar a la demostración del origen de los campos de fuerza, deberemos aceptar
el hecho de que todas las partículas subatómicas se componen de cargas eléctricas
elementales positivas y negativas, incluyendo aquellas que no presentan carga neta, tales
como los neutrones y neutrinos.
Cuando la cantidad de cargas positivas iguala a la de cargas negativas, resultan
partículas neutras. En el caso de que no exista equilibrio de cargas eléctricas, resultarán
partículas con carga neta positiva o negativa, de acuerdo con las cargas en exceso.
También deberemos considerar que en el interior de las partículas subatómicas no se
intercala el éter y sus componentes elementales tienen entre sí un contacto directo o
absoluto.
Sabemos que la densidad de las partículas subatómicas es enormemente alta. Basta
considerar el pequeño tamaño de los núcleos respecto al átomo. Actualmente se estima
esta densidad en 1014gr/cm3.
Hasta ahora se ha considerado que un cuerpo en equilibrio eléctrico no ejerce ninguna
fuerza eléctrica sobre otro cuerpo también neutro. Esto solo es cierto para grandes
distancias relativas, cuando la distancia entre las cargas eléctricas elementales resulta
despreciable respecto a la distancia entre los dos cuerpos, pero es falso en las distancias
pequeñas y más aún en el contacto absoluto.
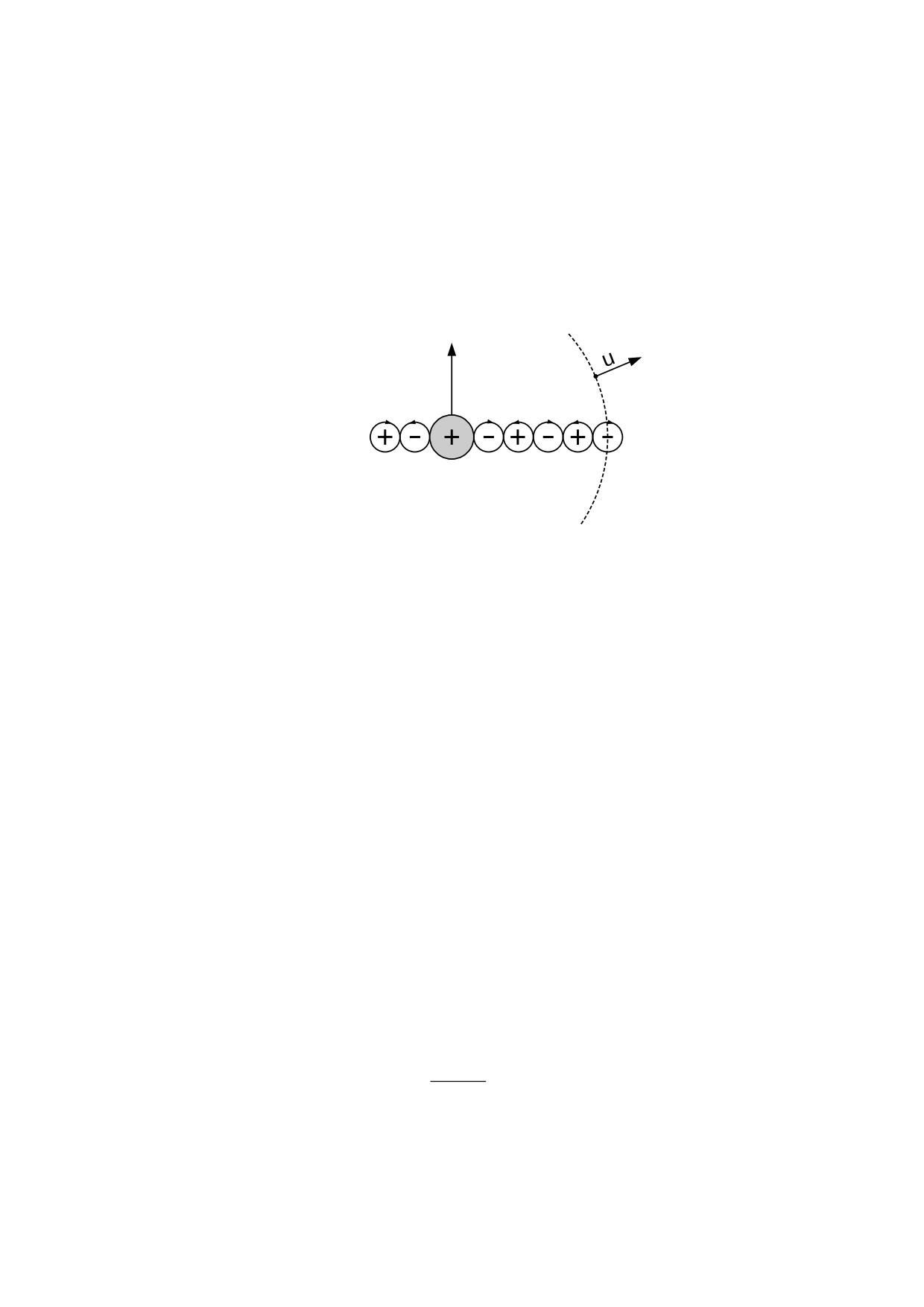
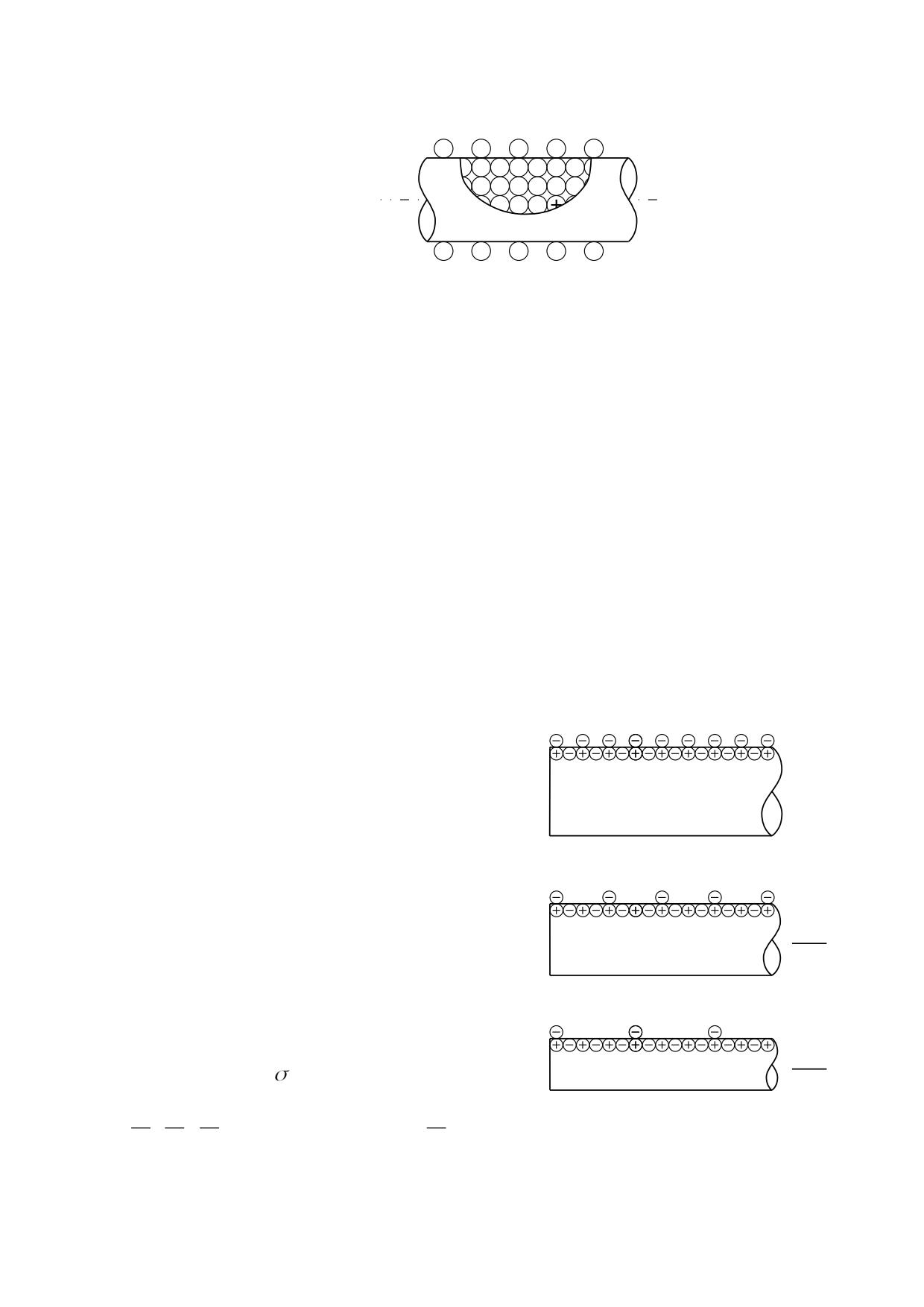
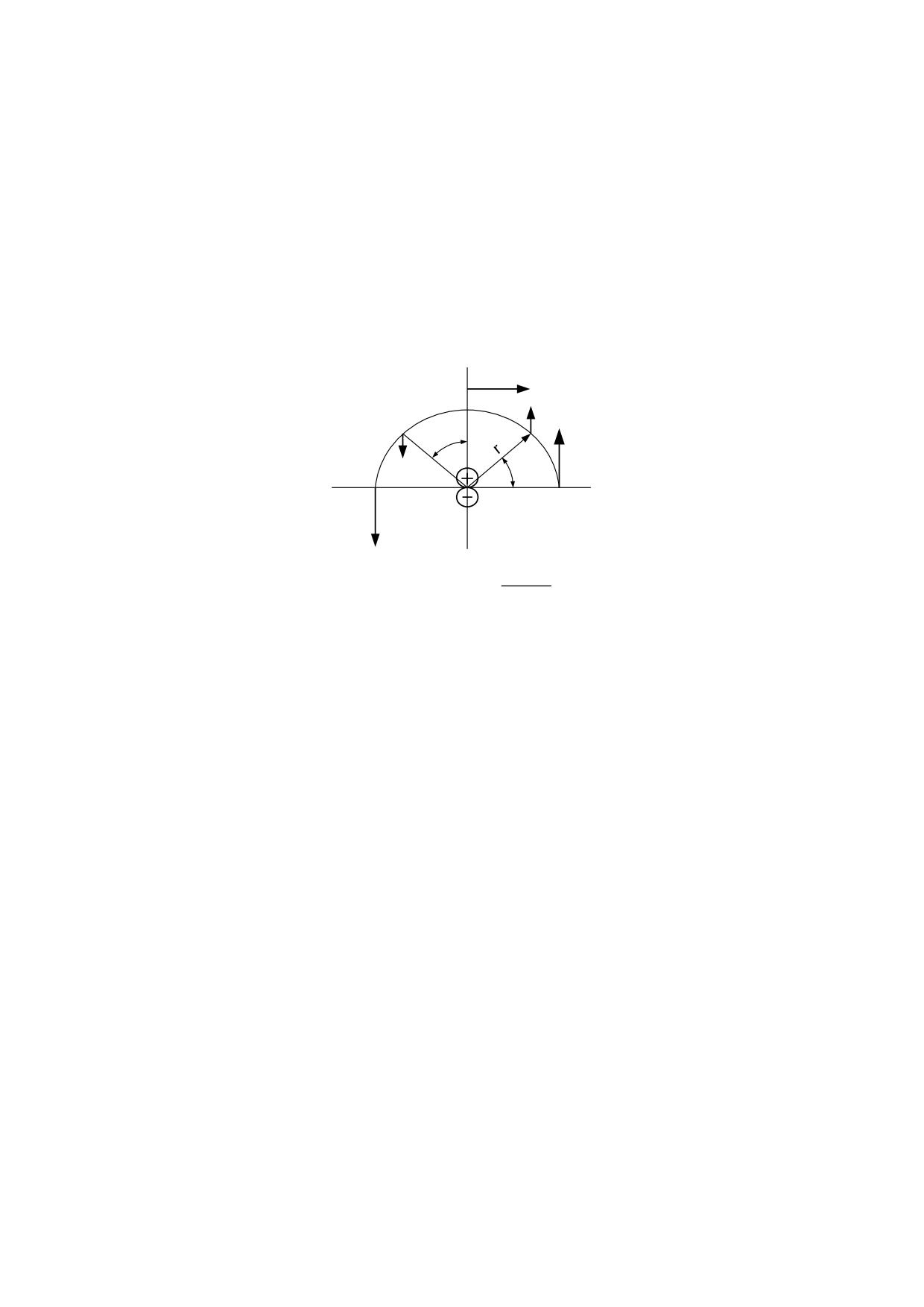
En la figura 2.3.1 se representan dos partículas neutras mostrando las cargas eléctricas
elementales, que están dispuestas alternativamente sobre la superficie. Se demuestra
aplicando las leyes electrostáticas que cuando la distancia que separa las dos partículas
es mayor que la distancia entre los centros de las cargas elementales, el campo
eléctrico queda anulado, pero a distancias menores que la mencionada el campo eléctrico
aumentará a medida que disminuya la distancia.
r
fig. 2.3.1
Cuando se realiza un contacto absoluto entre dos
partículas, como muestra la fig. 2.3.2 se enfrentan entre sí
las cargas elementales de signos opuestos,
produciéndose entre ellas una fuerza de cohesión de valor
máximo, a pesar de que las dos partículas son neutras.
Nos encontramos ante la fuerza más poderosa de la
Naturaleza, que además es la causante de todas las
fig. 2.3.2
fuerzas que conocemos, como podremos demostrar.
La fuerza resultante en el contacto es proporcional al producto de la densidad de las
masas y el área de la superficie de contacto.
F = K1 ρ1 ρ2 A
(2.3.1)
Donde: K1 = constante coeléctrica; y ρ = densidad de masa.
A la fuerza de contacto absoluto entre partículas que queda definida por la ecuación 2.3.1
la denominaremos en adelante “fuerza coeléctrica” para distinguirlo de la fuerza eléctrica.
Esta fuerza coeléctrica, cuando es ejercida por mediación del éter, es la causante del
campo gravitatorio, del campo eléctrico y del campo magnético, dependiendo del tipo de
alteración que produce en el éter, según demostraremos en los capítulos
correspondientes.
La certeza de la proposición de la ecuación 2.3.1 quedará demostrada al tratar el campo
gravitatorio y el campo eléctrico, donde comprobaremos que a partir de dicha ecuación se
llega hasta las ecuaciones clásicas.
En la ecuación 2.3.1 K1 es un factor de proporcionalidad que denominaremos constante
coeléctrica, mientras ρ1 y ρ2 son las densidades de masa respectivas de las dos partes
que toman contacto absoluto.
La razón por la cual la fuerza coeléctrica depende de la densidad de masa, es que la
carga eléctrica de las partículas elementales es proporcional a la masa de las mismas.
Es necesario asumir que lo que denominamos contacto absoluto difiere esencialmente de
lo que ordinariamente significa el contacto entre dos cuerpos, pues sabemos que en este
último caso las partículas mantienen una gran separación entre ellas. Basta con recordar
la distancia entre los núcleos de los átomos y los electrones.
La fuerza coeléctrica entre partículas con carga neta es independiente de su carga y de
su signo. Existe la misma fuerza coeléctrica entre dos protones que entre un protón y un
neutrón, o entre dos neutrones. Esto obedece a que la carga neta, al ser una carga
superficial queda desplazada de la zona de contacto, en la cual se enfrentan únicamente
las cargas de signo opuesto. Por otro lado veremos seguidamente que la repulsión de las
cargas del mismo signo no existe como una propiedad intrínseca de las mismas, pues es
un fenómeno que solo se produce a distancia, por mediación del éter.
2.4. Repulsión de cargas eléctricas.
Es el momento oportuno para aclarar un concepto erróneo asumido por la física clásica, al
considerar que las cargas eléctricas del mismo signo siempre se repelen entre sí. Esto es
cierto únicamente para la fuerza ejercida a distancia por mediación del éter, pero no es
una propiedad intrínseca de las cargas eléctricas. La realidad es que en el contacto
absoluto las cargas de distinto signo sufren una fuerza de cohesión, mientras que las del
mismo signo no sufren ningún efecto, lo cual es suficiente para explicar los fenómenos
eléctricos, como será demostrado.
Si reunimos una cantidad grande de cargas eléctricas de
un signo con otra cantidad diferente de signo contrario, se
agruparán hasta conseguir el equilibrio formando una red
cúbica como la representada en la fig. 2.4.1. Todas las
cargas sobrantes en este equilibrio se desplazarán hasta
la superficie empujadas por las otras cargas, donde
quedarán retenidas por la fuerza coeléctrica mientras la
superficie no se sature. Estas cargas superficiales
fig. 2.4.1
determinan el signo de la partícula.
Cuando una carga esté separada de la superficie de la partícula y tenga el mismo signo
que ésta, tenderá a separarse a causa de la polarización que se produce en el éter, como
se demostrará al tratar el campo eléctrico. Este resultado se ha considerado como una
fuerza de repulsión, aunque no es una propiedad intrínseca de las cargas eléctricas.
Un corcho sumergido en el agua sufre un empuje en sentido contrario a la fuerza de la
gravedad, pero a nadie se le ha ocurrido pensar que el corcho es repelido por la Tierra.
Sin embargo, esa sería la conclusión a la que habríamos llegado si los seres humanos
hubiésemos vivido sumergidos en compañía de los peces, sin conocer el mundo que
existe al otro lado de la superficie del agua.
2.5. Partículas subatómicas.
Anteriormente ya hemos descrito las denominadas partículas subatómicas como una
aglomeración de cargas eléctricas elementales de ambos signos, ordenadas en forma de
red cúbica y también se ha explicado que en las partículas con carga neta ésta queda
depositada en la superficie, como es el caso de los protones, electrones, etc.
En la fig. 2.4.1. se ha representado una sección de una partícula negativa constituida por
un pequeño número de elementos para facilitar la presentación, pero deberemos entender
que el número de cargas elementales debe ser muy elevado de modo que el conjunto
resultará de forma esférica.
El hecho de que las partículas subatómicas estén compuestas de cargas eléctricas
elementales explica la gran variedad de átomos que existen y además ayuda a entender
los fenómenos de desintegración atómica o la fusión de los átomos.
La fuerza que retiene una partícula subatómica en la superficie de un núcleo compuesto,
tendrá un límite determinado por la cantidad de elementos con los cuales tome contacto.
En el caso de partículas iguales de forma esférica, se demuestra que esta cantidad no
puede ser superior a 9, por lo tanto la fuerza no aumentará a partir de este límite, aunque
el número total de partículas que constituyen el núcleo sea muy elevado.
En la actualidad no sabemos por qué hay núcleos atómicos que son estables y otros que
tienen una vida efímera.
También resulta intrigante el hecho de que la carga positiva de un protón es igual a la
carga negativa de un electrón, mientras su masa es 1.836 veces mayor.
Es costumbre imaginar que todas las partículas subatómicas tienen forma esférica, pero
no hay razón alguna que nos obligue a pensar que debe ser así en todos los casos. En el
capítulo 10 el autor expone una teoría sobre la forma de los electrones que difiere mucho
del concepto clásico y de algunas hipótesis modernas.
La experiencia demuestra que en los núcleos atómicos, las cargas eléctricas positivas de
los protones no son capaces de producir la repulsión que les correspondería de acuerdo
con su signo, por lo cual ha sido necesario invocar la existencia de una “fuerza nuclear
intensa” para poder explicar este comportamiento. Sin embargo no se han podido
determinar las leyes de este campo de fuerza. La explicación es muy sencilla: los
protones en contacto absoluto no son repelidos porque no existe la repulsión intrínseca
entre las cargas del mismo signo, de acuerdo con la proposición del apartado 2.4. es la
fuerza coeléctrica la única con efecto.
A las cargas eléctricas elementales que componen las partículas subatómicas las
denominaremos en adelante “electrinos”, ya sean positivos o negativos.
Estos electrinos los consideraremos las partículas más pequeñas en que se puede dividir
la materia, hasta que el avance científico nos demuestre que pudieran estar constituidos
por elementos más pequeños. La historia nos ha demostrado que a medida que se han
perfeccionado los medios de observación, el tamaño de lo “indivisible” ha ido
disminuyendo cada vez más, mientras el tamaño del universo parece haber aumentado.
A la materia que constituye las partículas subatómicas, y por consiguiente los electrinos,
la denominaremos “materia compacta” para distinguirla de la materia ordinaria.
A esta materia compacta le adjudicaremos una densidad máxima y constante, según se
ha podido comprobar en algunos experimentos y que ha sido estimada con un valor de
1014gr/cm3.
2.6. La fuerza coeléctrica en los núcleos atómicos.
La fuerza coeléctrica o fuerza de contacto absoluto, justifica el comportamiento de las
partículas que constituyen los núcleos de los átomos, en los cuales parece existir una
fuerza de gran magnitud que ha sido denominada “fuerza nuclear intensa” y sobre la cual
no ha sido posible establecer las leyes que la rigen.
A esta fuerza enigmática los físicos contemporáneos le adjudican las siguientes
características:
- Independencia de la carga eléctrica: la fuerza nuclear entre dos protones es la misma
que entre los neutrones o entre un protón y un neutrón.
- Saturación: en un núcleo que contiene muchos nucleones, cada nucleón se enlaza
solamente con unos pocos de los restantes nucleones.
- Corto alcance: a una distancia aproximada de 10-15m la fuerza nuclear intensa es
atractiva y unas diez veces superior que la fuerza eléctrica entre dos protones. La fuerza
disminuye rápidamente con la distancia creciente, haciéndose despreciable a quince
veces esta separación. Cuando dos nucleones están separados una distancia de
aproximadamente 0,4x10-15m la fuerza nuclear intensa se vuelve repulsiva. Estos
nucleones no colapsan.
Después de analizar las características que aparenta tener la “fuerza nuclear intensa”,
quedan pocas dudas de que esta fuerza es la misma cosa que nosotros hemos definido
como una fuerza de cohesión de contacto absoluto y que denominamos “fuerza
coeléctrica”.
Las dificultades que los investigadores encuentran para deducir las leyes que rigen este
nuevo campo de fuerza tienen su causa en el hecho de que no existe ningún campo de
fuerza, ya que la fuerza solo tiene efecto en el contacto directo de los elementos.
El conocimiento de la fuerza coeléctrica y la ausencia de la repulsión intrínseca de las
cargas eléctricas, permitirá una interpretación más correcta de los fenómenos que ocurren
en los núcleos atómicos.
2.7. Los diferentes campos de fuerza.
Conocemos la existencia de fuerzas que se producen a distancia, como son la fuerza
gravitatoria, la fuerza eléctrica y la fuerza magnética, que la física clásica explica por la
existencia de campos de fuerza, pero ignoramos cual es la naturaleza concreta de estos
campos. Además, en los últimos tiempos se han descubierto las “fuerzas nucleares
intensas” y “las fuerzas nucleares débiles”, las cuales resultan más enigmáticas todavía
que las anteriores.
A lo largo de este tratado se demostrará que esencialmente solo existe una fuerza única,
que es la fuerza coeléctrica, y que todas las demás son una consecuencia de esta última
cuando se ejerce por mediación del éter, el cual puede ser alterado de distintos modos,
dando lugar a los diferentes campos de fuerza.
La fuerza gravitatoria se produce como consecuencia del contacto del éter con las
partículas de masa, cuando la densidad del éter ha sido alterada originando un gradiente
de densidad.
La fuerza eléctrica se produce por el contacto del éter con las partículas que tienen carga
eléctrica neta, cuando el éter sufre un desplazamiento dieléctrico en sus eterones.
La fuerza magnética resulta del contacto del éter con las cargas eléctricas en movimiento,
cuando los eterones están sometidos a un movimiento de rotación.
La fuerza nuclear débil es similar a la fuerza gravitatoria, pero es de corto alcance y tiene
una ley diferente. A esta fuerza la denominaremos “fuerza gravitónica” debido a su
relación con la fuerza gravitatoria.
La fuerza nuclear intensa es la misma que nosotros ya conocemos como fuerza
coeléctrica y sabemos que no constituye ningún campo de fuerza, pues solo tiene efecto
por el contacto directo.
El campo magnético se diferencia de los demás en que debe su existencia al movimiento
de la materia, mientras los otros pueden existir en situaciones estáticas.
3.1. La fuerza gravitatoria.
La experiencia demuestra que la masa de los cuerpos produce una fuerza de atracción
entre ellos y Newton demostró que esta fuerza se rige por la siguiente ley:
m1 m2G
F=
r2
en la cual G es un factor constante conocido como constante gravitatoria y r es la
distancia que separa el centro de gravedad de las masas.
A pesar de conocerse la ley que rige esta fuerza, nunca se ha podido explicar como se
puede producir esta fuerza a través del espacio vacío.
La explicación es que la fuerza no se produce a través del vacío. Es el éter el que
realmente produce la fuerza por acción directa, actuando como intermediario, de la
manera siguiente:
Una masa produce una alteración en la densidad del éter inmediato creando un gradiente
de densidad en el mismo, y a su vez este gradiente produce sobre otra masa un
desequilibrio en las fuerzas coeléctricas de contacto con el éter, dando por resultado una
fuerza orientada en el sentido del gradiente. La afirmación de que la fuerza se dirige hacia
la otra masa solo es cierta en el caso de que esta se encuentre en reposo respecto al
éter, pues el campo gravitatorio necesita un tiempo para desplazarse y en este tiempo la
masa habrá cambiado su posición, de acuerdo con su velocidad.
F
m2
m1
fig. 3.1.1
3.2. El gradiente de densidad en el éter.
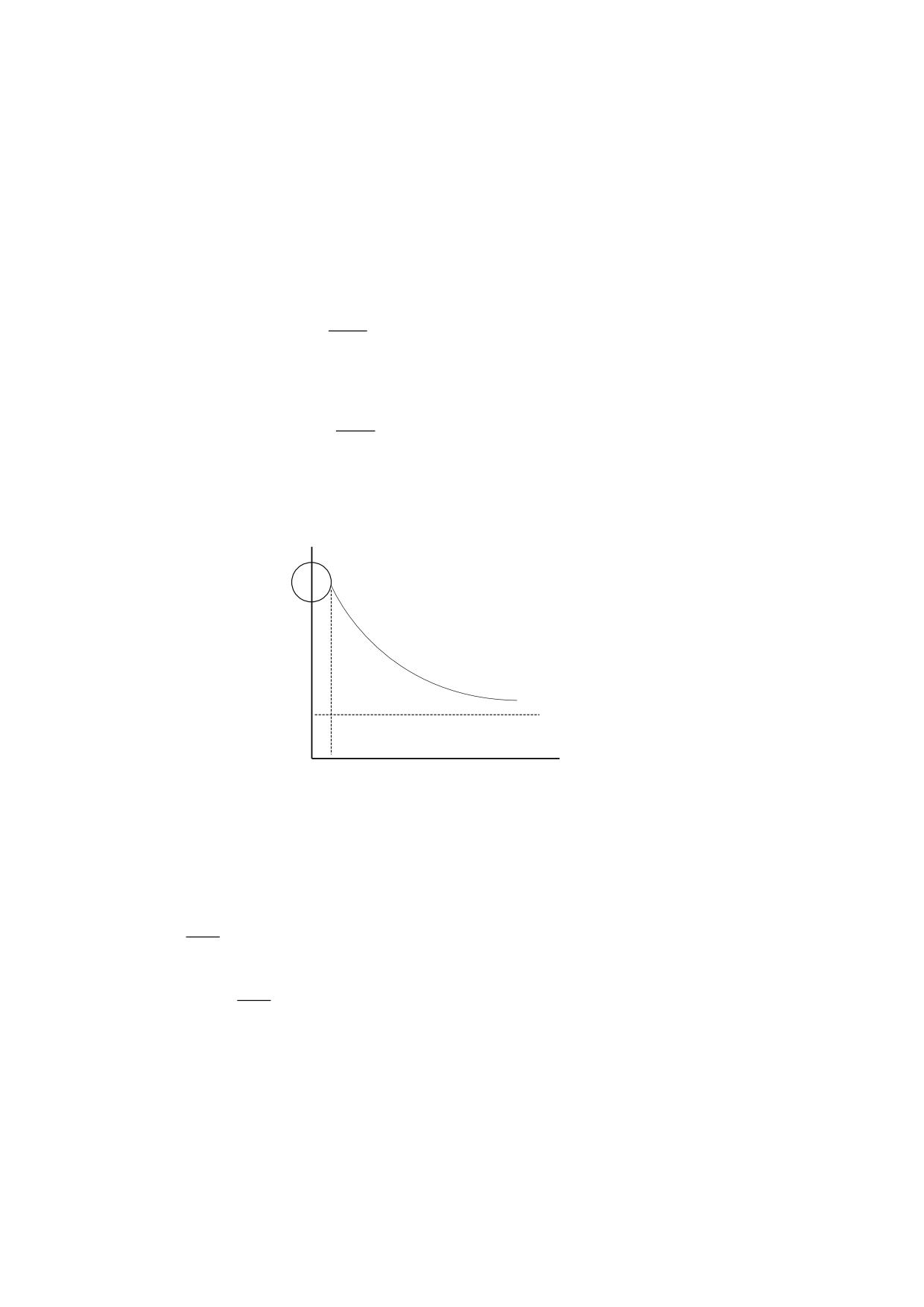
En cada región del espacio la densidad del éter tiene un valor básico (ρb) que depende de
la distribución de las masas en el universo. Esta densidad básica resulta alterada por la
presencia de una masa en razón directa de la magnitud de la masa y en razón inversa de
la distancia de su centro de gravedad.
La magnitud de la alteración obedece a la siguiente ecuación:
K2m
Δρ=
(3.2.1)
r
La densidad absoluta resultará:
K2m
ρ=ρb+
(3.2.2)
r
Donde el factor K2 es una constante de densidad y ρb es la densidad básica en la región
tratada.
ρ
m
ρb
0
r
fig. 3.2.1
La alteración de la densidad provocada por la presencia de una masa tiene un gradiente
(gp) que está determinado por la derivada de la densidad respecto a la distancia:
k2m
∂ρ
Para: Δρ=
resulta:
gρ=
r
∂r
k2m
Por lo tanto: gρ=
(3.2.3)
r2
Gm
En la física clásica la intensidad del campo gravitatorio está definida por:
g=
r2
Comparando estas dos últimas ecuaciones vemos que solo difieren en los factores
constantes K2 y G, lo cual demuestra que el gradiente de densidad y la intensidad del
campo gravitatorio son proporcionales.
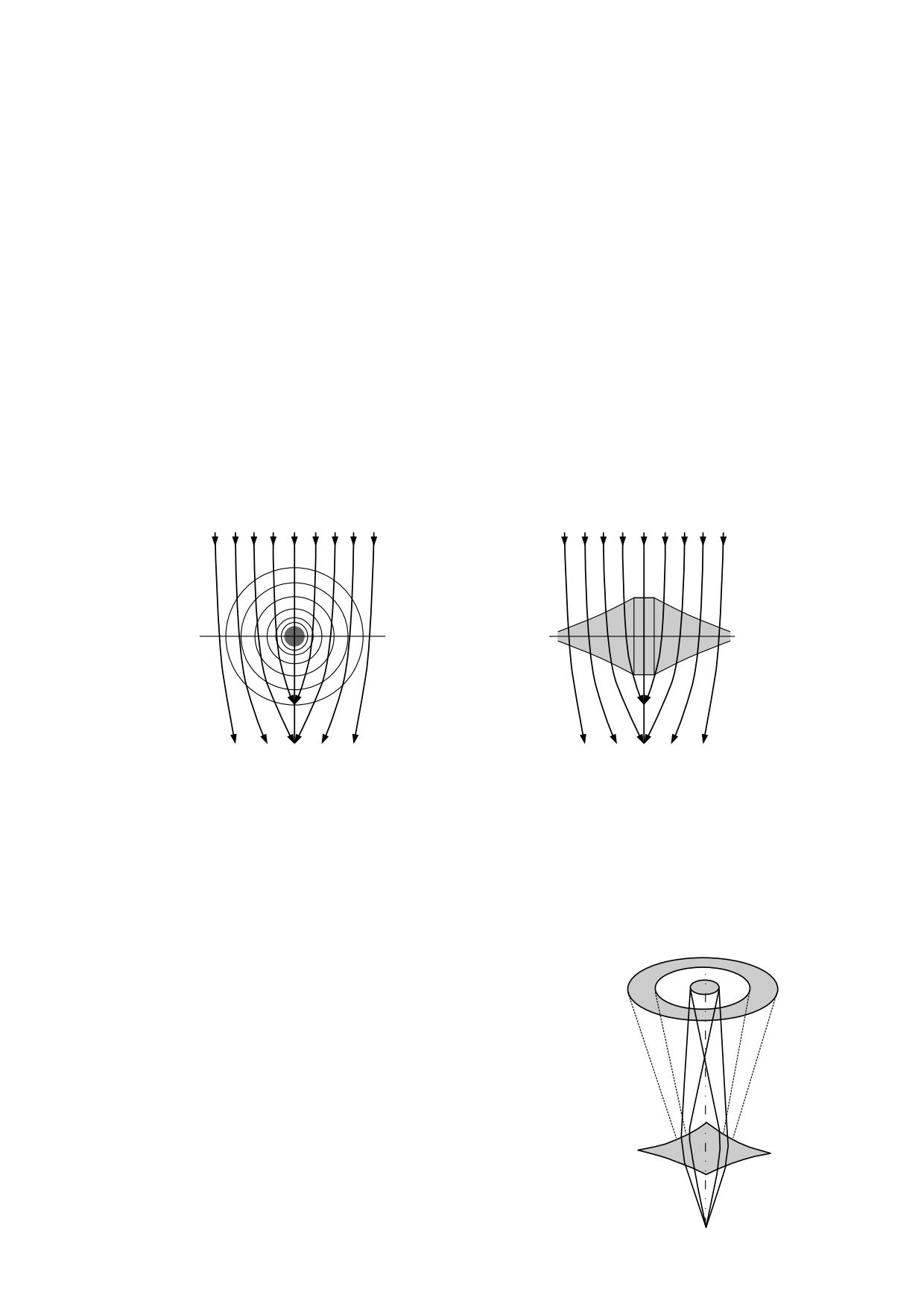
3.3. Fuerza gravitatoria producida por el éter.
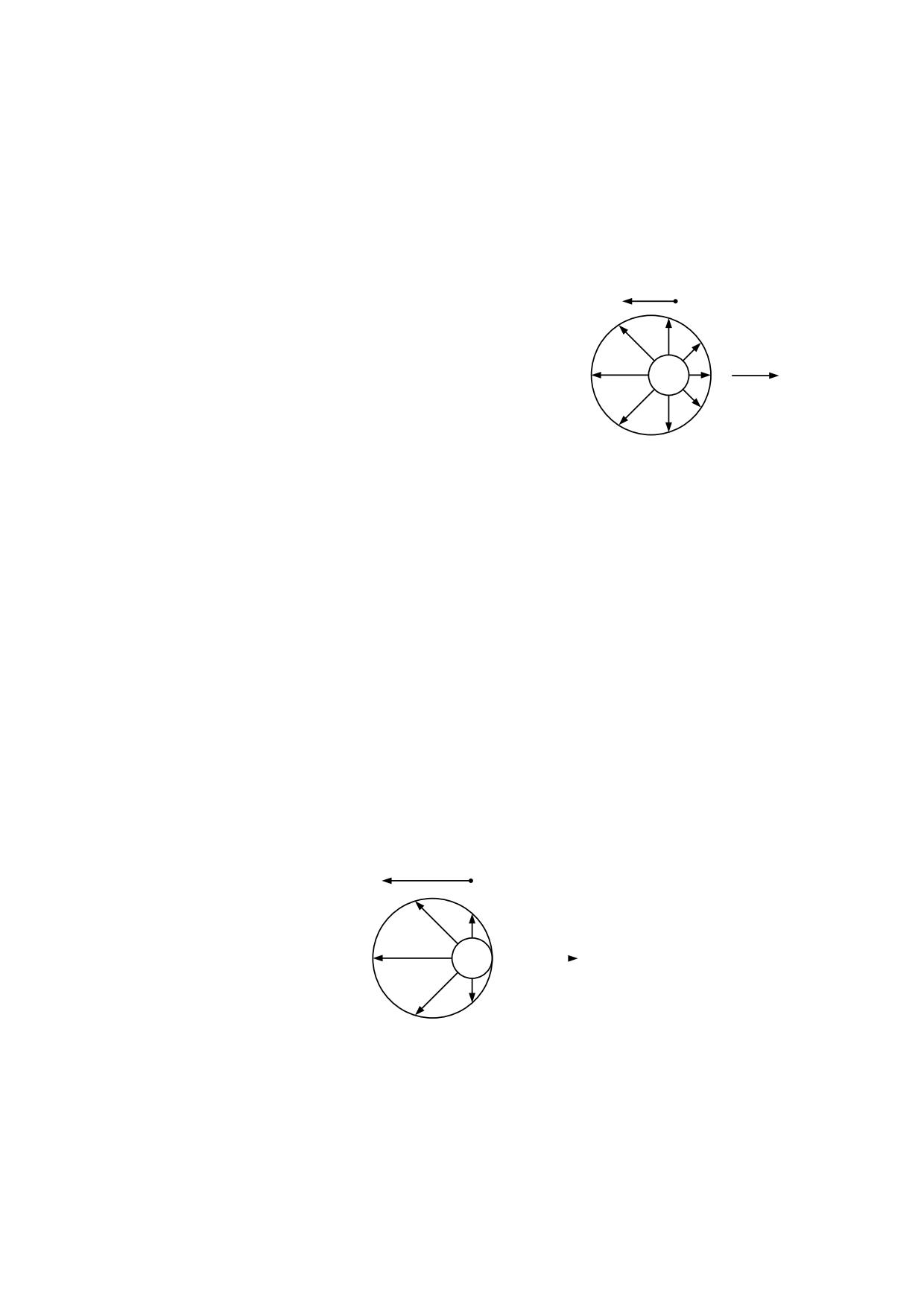
Una partícula de masa inmersa en el éter sufre en su superficie unas fuerzas coeléctricas
proporcionales a la densidad del éter con el que toma contacto. Solamente ejercen fuerza
los eterones que están en contacto directo con la superficie de la partícula.
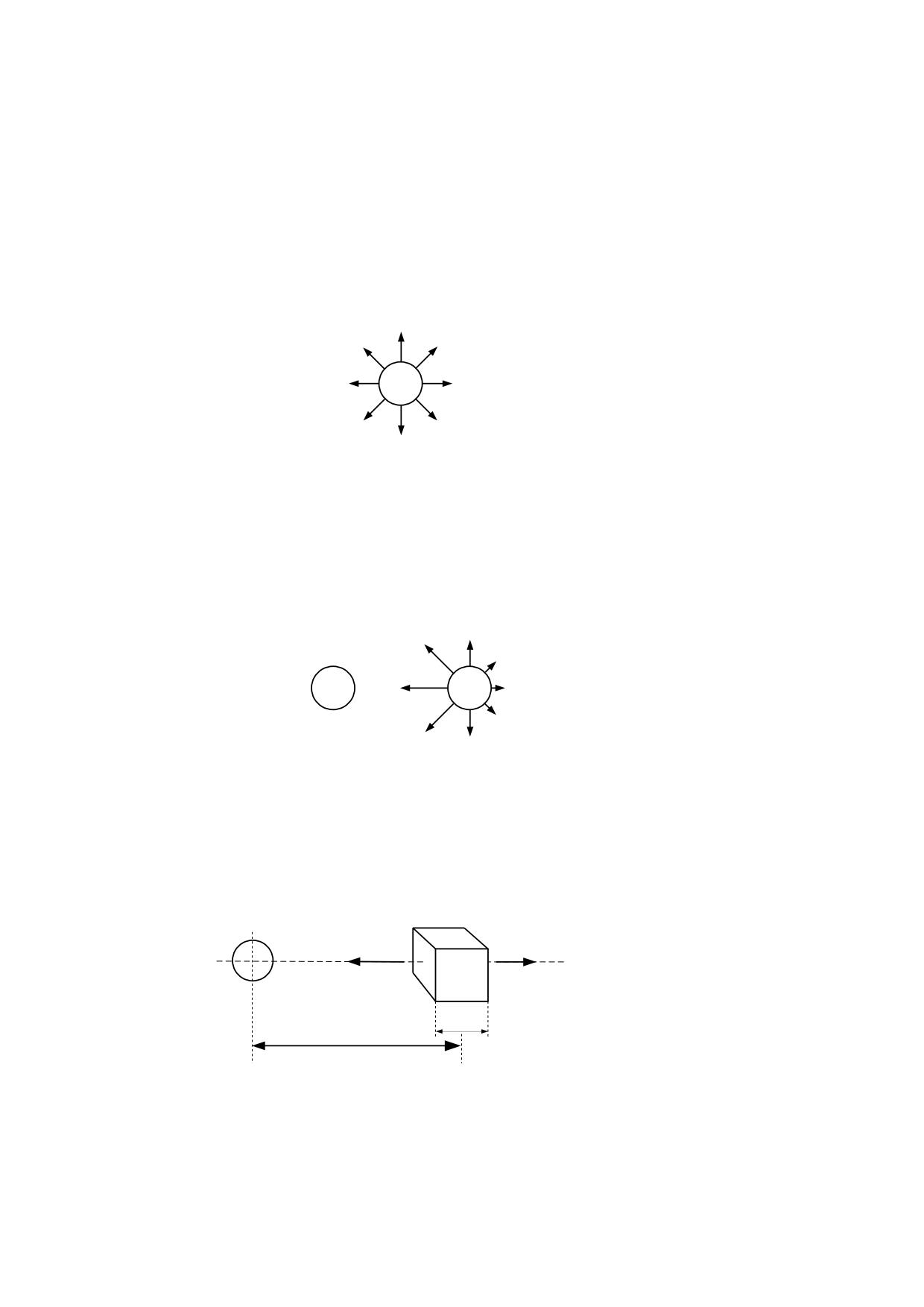
En ausencia de campo gravitatorio la densidad del éter es uniforme y por lo tanto la
partícula sufre fuerzas iguales en todas las direcciones, de modo que quedan
equilibradas, según se representa en la fig. 3.3.1.
fig. 3.3.1
Sin embargo la presencia de otra masa provoca un gradiente de densidad en el éter y
como consecuencia de este gradiente las fuerzas coeléctricas quedan desequilibradas,
produciendo una fuerza resultante dirigida hacia el lado de mayor densidad de acuerdo
con la fig. 3.3.2. Seguidamente vamos a determinar el valor de la fuerza que se origina
entre dos masas, en función de la magnitud de estas y de la distancia que las separa.
m1
m2
fig. 3.3.2
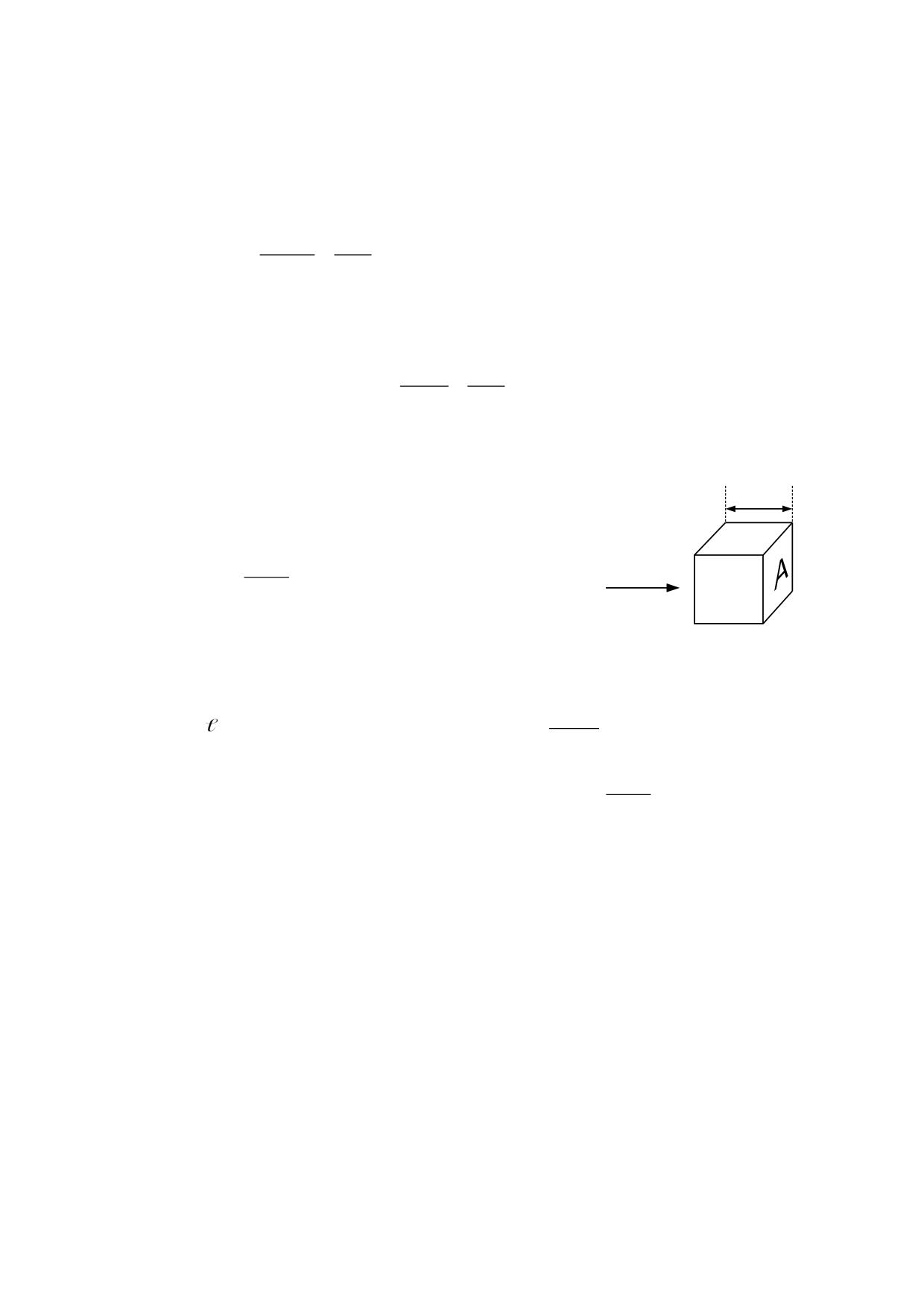
Para facilitar la demostración vamos a considerar que la masa m2 tiene forma cúbica y
está orientada con uno de sus ejes en la dirección del gradiente, tal como ilustra la fig.
3.3.3.
m2
m1
F2
F1
ρ1
ρ2
dr
r
fig. 3.3.3
Sabemos que la fuerza coeléctrica obedece a la ecuación 2.3.1. que dice: F = K1ρ1ρ2A.
Para adaptarla a las condiciones del caso la escribiremos: F = ρeρmAK1, donde ρe es la
densidad del éter, ρm es la densidad de la masa y K1 es la constante coeléctrica. En la
figura 3.3.3 observamos que ρ1 = densidad en cara 1; y ρ2 = densidad en cara 2.
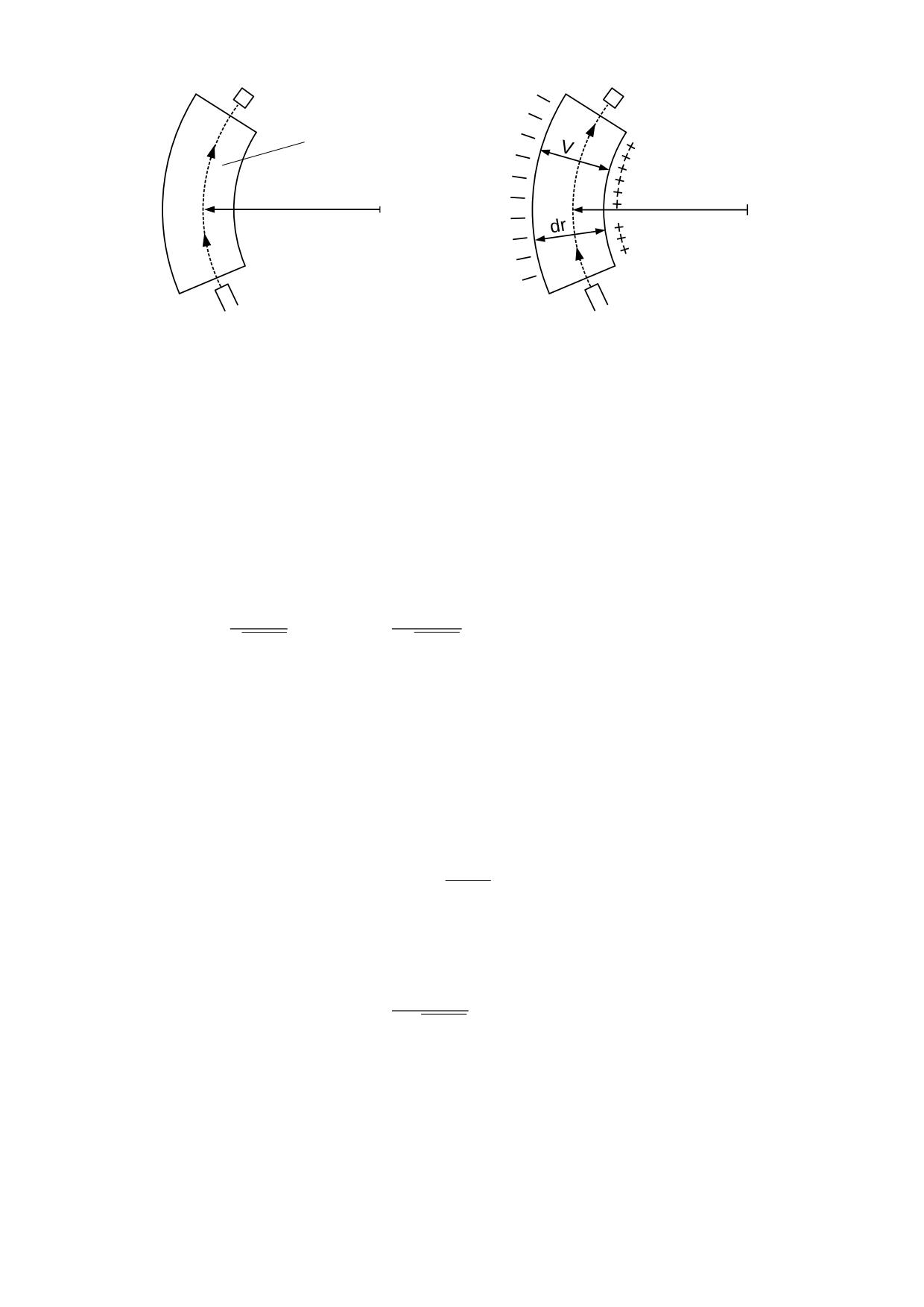
Observando la fig. 3.3.3 deducimos que las fuerzas coeléctricas estarán equilibradas en
todas las caras del cubo excepto en las 1 y 2, en las cuales se producen las fuerzas F1 y
F2 de distinto valor debido al gradiente del éter:
F1 = ρ1 ρm A K1
F2 = ρ2 ρm A K1
La fuerza resultante sobre la masa será F = F1 - F2 y por consiguiente:
F = ρ1 ρm A K1 - ρ2 ρm A K1 = (ρ1-ρ2) ρm A K1
Pero ρ1 - ρ2 = δρ , luego F = δρ ρm A K1
(3.3.1)
El gradiente de densidad provocado por la masa m, obedece a la ecuación 3.2.3 que
expresa:
k2m
gρ=
r2
K2mδr
La diferencia de densidad en la distancia δr será δρ = gp δr, luego
δρ=
;
r2
y por consiguiente la fuerza resultante sobre m2 de acuerdo con la ecuación 3.3.1 será:
K2m1
δr
m1 K1 K2
F = δρρm AK1 =
ρm AK1 =
ρm Aδr
r2
r2
pero Aδr resulta ser el volumen de m2, luego ρm A δr = m2 ;
m1m2 K1 K2
y por consiguiente: F=
(3.3.2)
r2
G
m1m2
La ley de Newton es: F=
r2
G = 6,67x10-8dinas cm2/g2
G = 6,67x10-11N m2/kg2
Si consideramos que K1K2 = G ambas ecuaciones son equivalentes, quedando
demostrado que la fuerza gravitatoria se produce a causa del gradiente del éter y de la
fuerza coeléctrica.
La demostración anterior pudiera parecer un tanto artificiosa, pero sin embargo es
equivalente a la que demuestra el conocido principio de Arquímedes. La única diferencia
es que ahora tratamos con fuerzas de cohesión y en el principio de Arquímedes era con
fuerzas de empuje.
Se puede demostrar que la fuerza de atracción que sufre un volumen determinado de éter
en un campo gravitatorio es la misma pero con sentido contrario que la fuerza de empuje
que produce el gradiente de presión del éter según el principio de Arquímedes, que es la
condición necesaria para un estado de equilibrio.
Newton manifestó en alguna ocasión su insatisfacción porque su teoría de la gravitación
parecía incompatible con su principio de acción y reacción. La teoría del éter satisface
plenamente esa compatibilidad porque la reacción se produce sobre el éter. ¡Newton tenía
razón en sus dudas!
3.4. Intensidad del campo gravitatorio.
La intensidad del campo se define como la medida de la fuerza gravitatoria ejercida sobre
una unidad de masa:
m1m2
G
m1G
F
g=
F=
luego g=
(3.41)
m2
r2
r2
m1 K1 K2
como G = K1K2 ; resulta
g=
(3.4.2)
r2
m1 K2
pero el gradiente de densidad es gρ=
:
r2
por consiguiente resulta que g=gρK1
(3.4.3)
Por lo tanto podemos afirmar que la intensidad del campo gravitatorio es el producto del
gradiente de densidad del éter y la constante coeléctrica.
La física clásica nos demuestra que la aceleración que sufre una masa cualquiera
sometida a un campo gravitatorio tiene el mismo valor que la intensidad de campo, con
independencia de cual sea la magnitud de la masa.
m1m2
G
gm2
F
a=
F=
=g m2
a=
=g
m2
r2
m2
Por consiguiente, a=g=gρK1
(3.4.4)
La aceleración es el producto del gradiente de densidad y la constante coeléctrica.
3.5. El potencial gravitatorio.
El potencial gravitatorio originado por una masa en un punto del espacio queda definido
en la física clásica por:
m1G
Vg=
(3.5.1)
r
Por otro lado el incremento de densidad provocado en el éter resulta:
m1 K2
Δρ=
r
Como la constante gravitatoria equivale a K1K2 tendremos:
m1 K1 K2
Vg=
r
De donde resulta que
Vg=ΔρK1
Esta ecuación significa que el potencial gravitatorio es el producto del incremento de la
densidad del éter y la constante coeléctrica.
4.1. Una fuerza diferente.
Son varias las razones que nos inducen a pensar que en las proximidades de las
partículas subatómicas se produce un campo de fuerza distinto de los que hasta ahora se
han considerado.
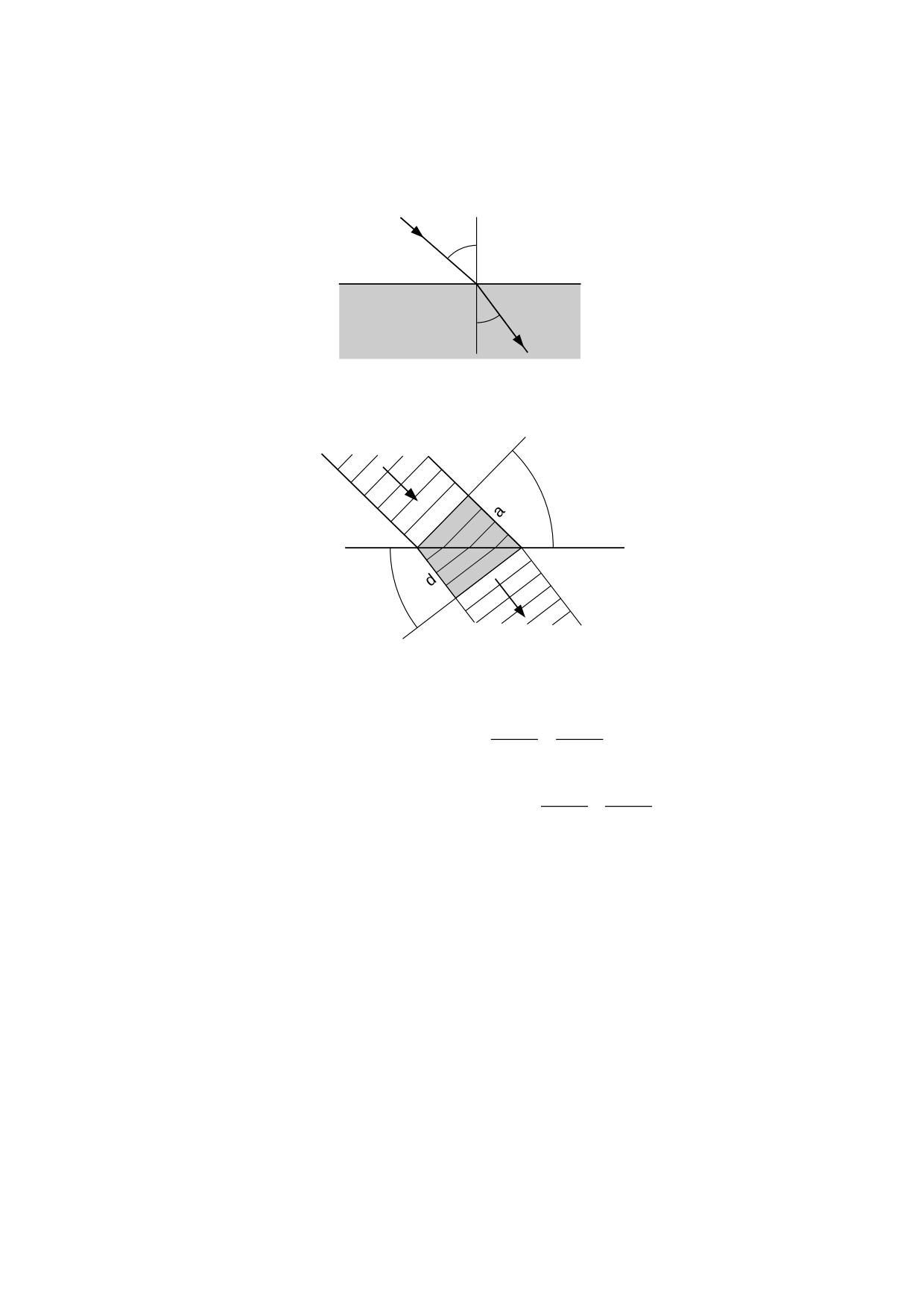
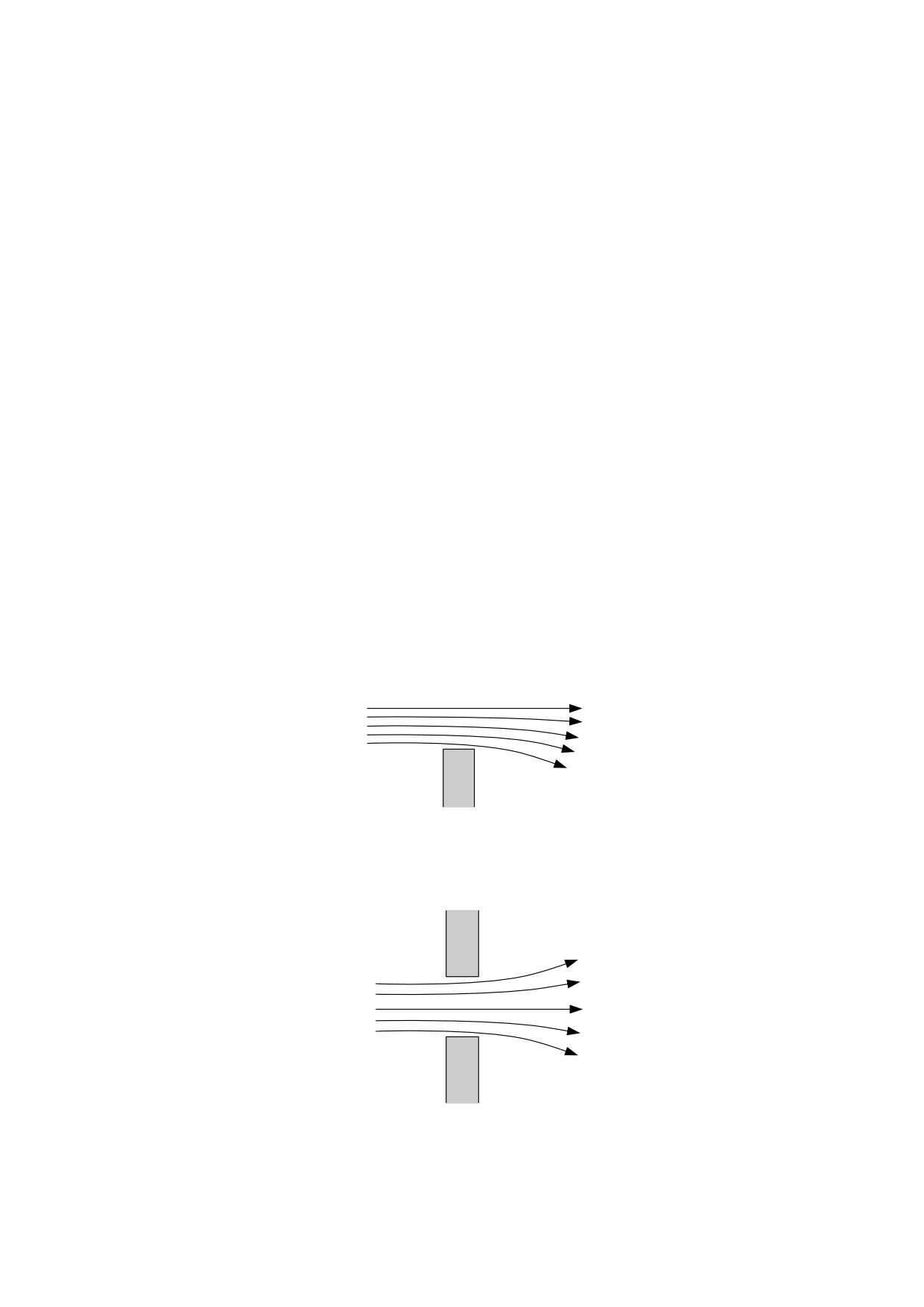
Una razón viene dada por el comportamiento de la luz cuando atraviesa un cuerpo
transparente. En el capítulo 7 se demostrará que la velocidad de las ondas
electromagnéticas depende de la densidad del éter de acuerdo con la ecuación 7.2.3,
pero el incremento de la densidad del éter debido al campo gravitatorio de las partículas
que constituyen el cuerpo sería insignificante para justificar el fenómeno de la refracción
óptica.
Por otro lado, la tentativa para explicar como se origina el campo gravitatorio a partir de
una masa, nos conduce a la conclusión de que en las proximidades de las partículas la
ley que rige el fenómeno debe ser diferente que la propia del campo gravitatorio.
Otra razón para presumir la existencia de este nuevo campo de fuerza es que puede
justificar de manera inmediata la fuerza de cohesión entre los átomos de los cuerpos
sólidos, sin recurrir a los oscuros conceptos de la mecánica cuántica.
Por último, sabemos que en la investigación nuclear se ha detectado la existencia de una
fuerza desconocida hasta ahora, denominada “fuerza nuclear débil” y cuyas leyes no han
sido encontradas.
La existencia del éter nos permite explicar este fenómeno, al cual denominaremos “campo
gravitónico” por estar relacionado con el campo gravitatorio.
La función que corresponde a esta fuerza tiene una gran importancia en las pequeñas
distancias, por lo cual permitirá una mejor interpretación de la mecánica de los átomos.
4.2. El campo gravitónico.
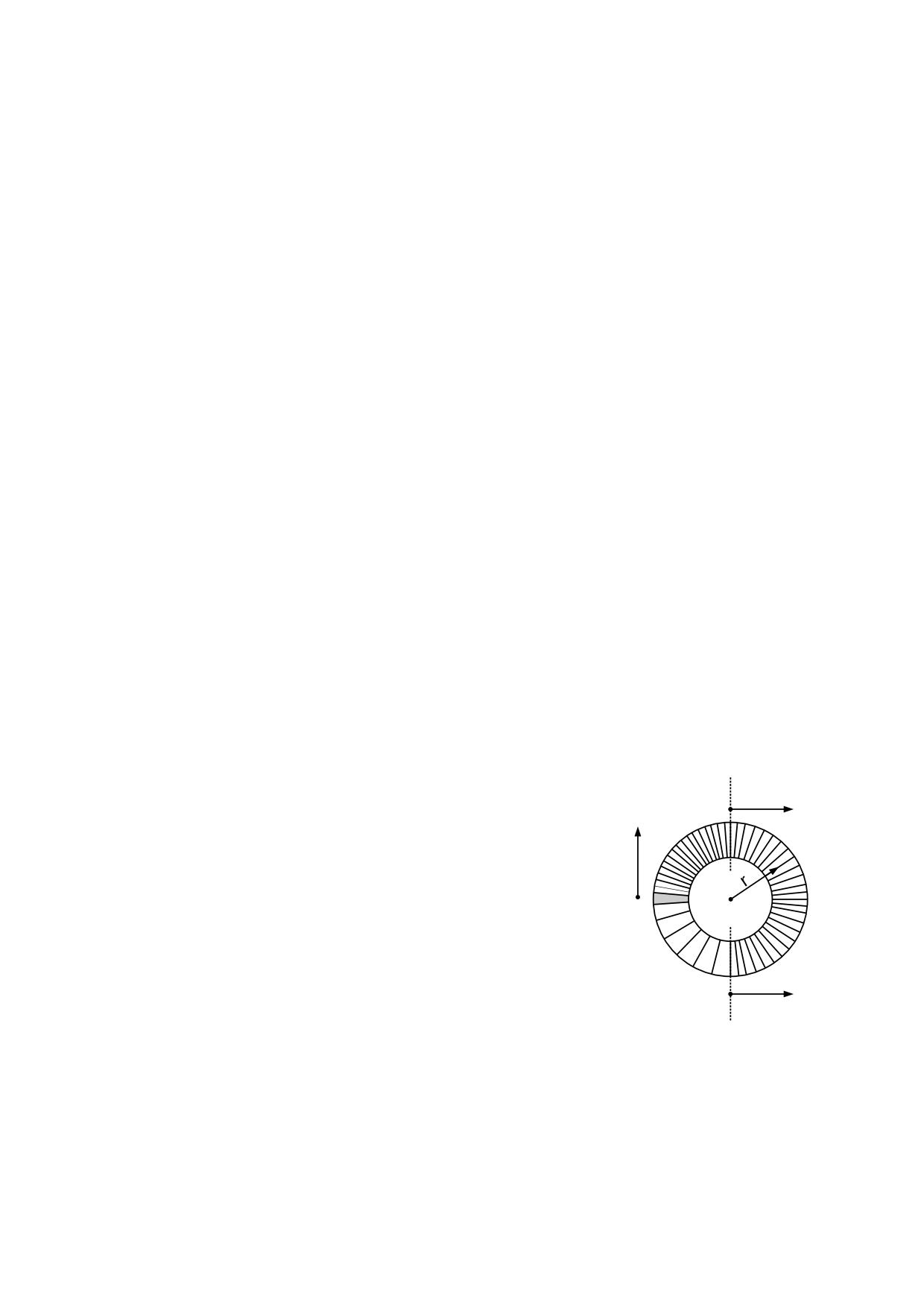
En el capítulo 2 describíamos la estructura del éter como una red cúbica, más o menos
deformada, constituida por eterones positivos alternados con eterones negativos, de
modo que los eterones contiguos deben tener signos opuestos.
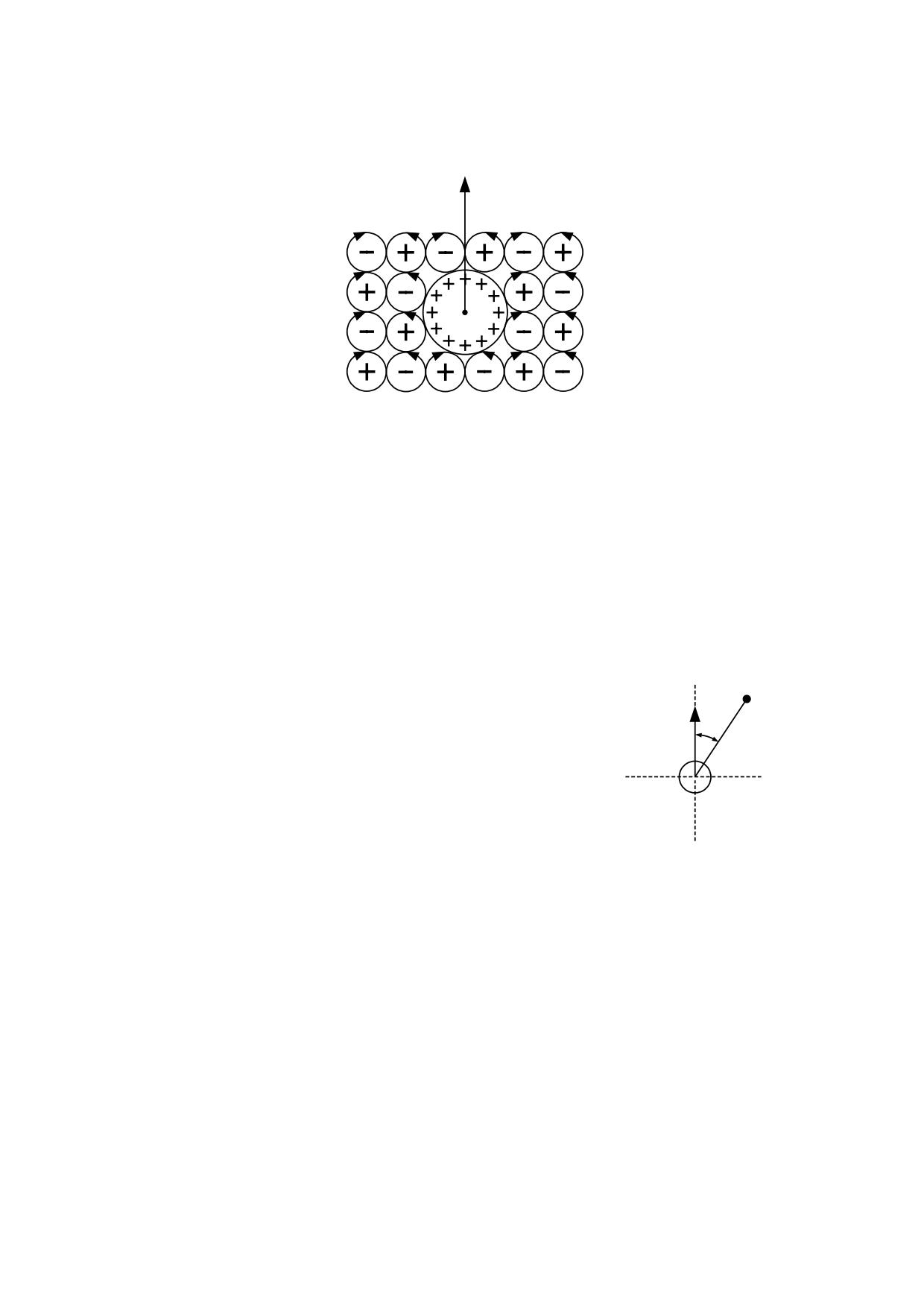
La presencia de una partícula de masa compacta en el seno del éter modificará la
distribución de los eterones, debido a la fuerza coeléctrica que se produce en la superficie
de contacto entre estos y los electrinos de signo contrario. La elasticidad de los eterones
permitirá que se compriman lo necesario para adaptarse al mosaico de electrinos que
cubren la superficie de la partícula, manteniendo al mismo tiempo una distribución
alternada de acuerdo con el signo de carga eléctrica, lo cual los forzará a una
configuración radial como la representada en la fig. 4.2.1 que es una sección que pasa
por el centro de la partícula compacta.
-
+
+
-
+
-
-
-
+
+
-
+
+
+
-
-
-
+
+
-
-
+
-
+
m
-
+
+
-
-
+
-
+
-
-
+
+
+ -
+
-
+
-
-
+
-
+
+
-
fig. 4.2.1
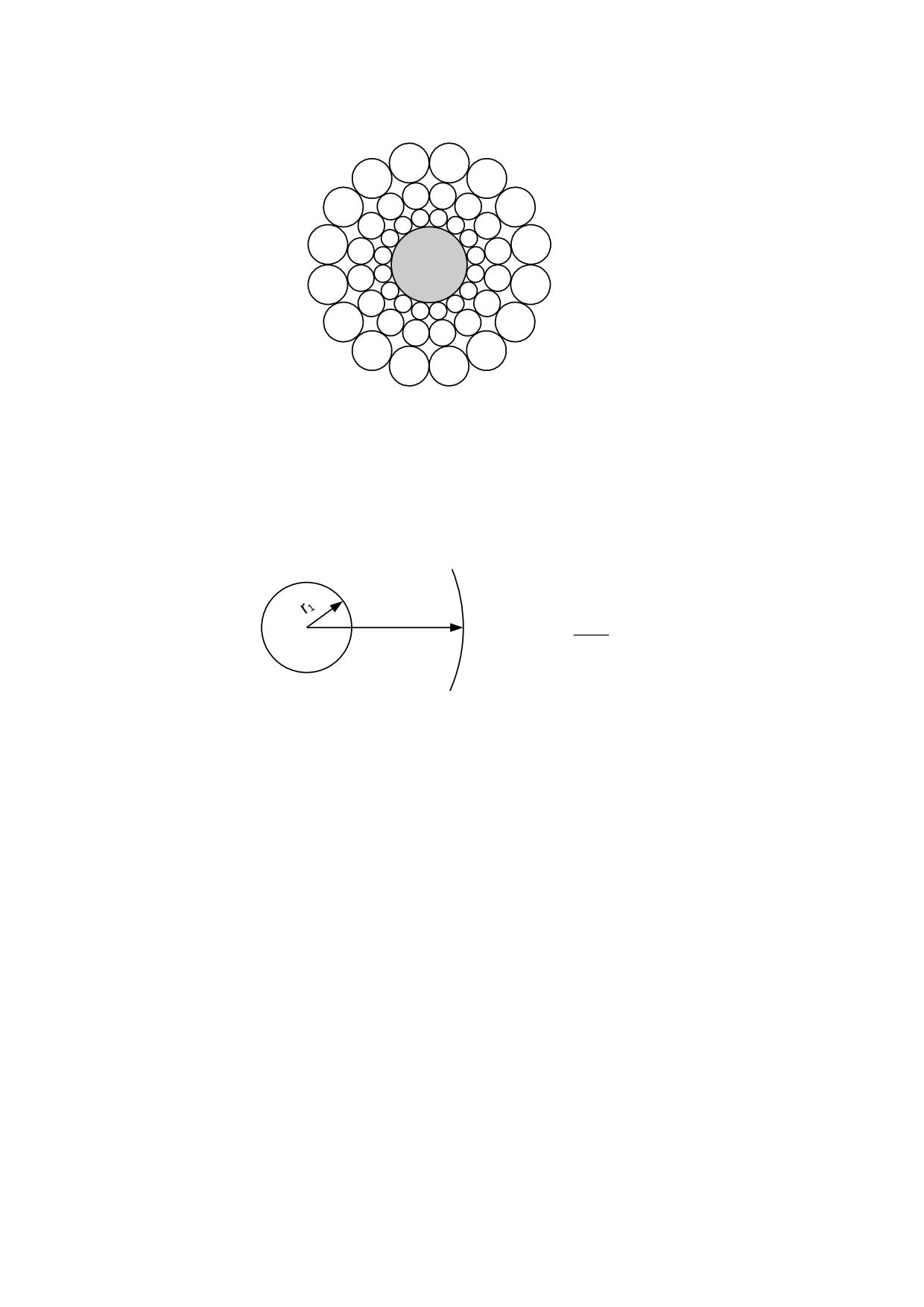
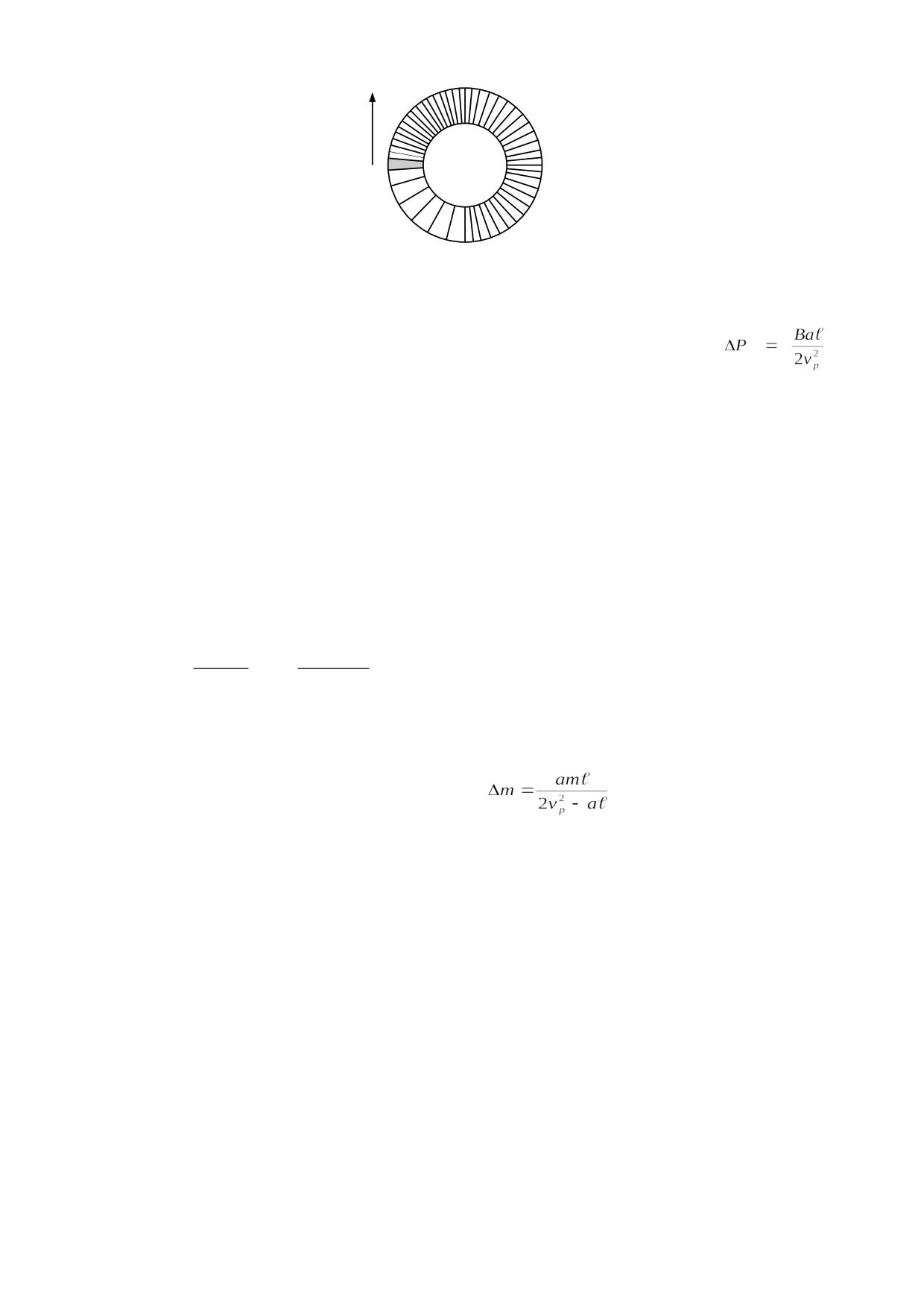
Esta distribución radial determina que el volumen de los eterones resulte proporcional a r3,
siendo r la distancia al centro de la masa y por consiguiente la densidad de los eterones
será inversamente proporcional a r3. Esto nos permite determinar la densidad relativa del
éter a cualquier distancia.
r2
3
ρ1r
1
ρ2=
(4.2.1)
ρ1
ρ
3
ρm
2
r
2
fig. 4.2.2
Donde ρ1 es la densidad del éter en la superficie de la partícula y ρ2 es la densidad a la
distancia r2 desde el centro de la misma.
Sabemos que la fuerza coeléctrica es una fuerza de cohesión producida por el contacto
absoluto entre las superficies de los cuerpos en función de la densidad de sus masas,
pero con independencia de la masa total de cada cuerpo.
Sin embargo habremos de demostrar que el efecto de la fuerza gravitónica, así como la
fuerza gravitatoria, que se producen a distancia por mediación del éter, resultan
dependientes de la magnitud de la masa.
Debido a que la densidad del éter resulta alterada por una partícula de masa compacta en
razón inversa a r3 y que la masa de la partícula es proporcional a r3 resulta que en la
superficie de la partícula esférica, la densidad del éter tendrá una magnitud constante
para cualquier tamaño de la partícula.
El asumir que la masa compacta tiene valor constante y que en la superficie de una
partícula compacta la densidad del éter alcanza también una magnitud constante nos va a
permitir que en la ecuación 4.2.1 sustituyamos el valor del radio de la partícula por la
masa de la misma:
4
4
3m
m=ρ
V
luego m=ρm
πr3
donde r3=
m
V=3πr13
3
4 πρm
Llevado este valor de
r3
a la ecuación 4.2.1 tendremos:
3m
ρ1
ρ2=
3
4 πρmr
2
Pero como ρ1 y ρm son valores constantes, nos permiten establecer una constante K3 que
denominaremos “constante de densidad gravitónica”:
3ρ1
K3m
K3m
K3 =
luego ρ2 =
y
ρ1 =
3
4 πρm
r3
r
1
K3m
Generalizando podemos escribir ρ=
(4.2.2)
r3
Como en cada región del universo el éter tiene una densidad propia que ya conocemos
como densidad básica (ρb) la presencia de una partícula con masa compacta incrementará
esta densidad, de modo que la densidad absoluta resultará:
K3m
ρ=ρb+
(4.2.3)
r3
Puesto que el incremento de densidad varía con la distancia a la partícula, se producirá
un gradiente de densidad cuyo valor será:
δρ
gρ=
δr
K3m
3K3m
δρ
Cuando Δρ=
; resultará
=
r3
δr
r4
Luego
(4.2.4)
Al estudiar el campo gravitatorio demostrábamos que sobre una masa inmersa en el éter,
con un gradiente de densidad, se produce una fuerza debida al desequilibrio de las
fuerzas coeléctricas producidas por el contacto del éter con dicha masa.
Siguiendo el mismo proceso que habíamos utilizado en el caso del campo gravitatorio, se
demuestra que la fuerza en un campo gravitónico deberá ser:
donde K1 es la constante coeléctrica y K3 es la constante de densidad gravitónica.
El producto de 3K3K1 es otra cantidad constante que designaremos con la legra J de modo
que la ecuación anterior se convierte en:
m1m2
J
F=
(4.25)
r4
A la constante J la denominaremos “constante gravitónica”.
Si definimos la intensidad del campo gravitónico como la fuerza ejercida sobre la unidad
de masa, y la designamos con la letra ĵ tendremos:
m1J
F
ĵ=
luego
ĵ=
(4.2.6)
m2
r4
En la actualidad no conocemos todavía el valor numérico de la constante gravitónica J
que deberá ser determinada experimentalmente, como sucedió con la constante
gravitatoria G, que no se conoció con precisión hasta que la midió Cavendish un siglo
después de que Newton propusiera la ley de la gravitación universal.
Por consiguiente no podemos calcular cual es la magnitud del campo gravitónico ĵ, pero
resulta evidente que a pequeñas distancias su valor resultará muy elevado, decreciendo
rápidamente al aumentar la distancia, como se deduce de la ecuación 4.2.6.
Podríamos aventurar la afirmación de que su intensidad se hace despreciable a una
distancia algo mayor que la que separa entre sí los átomos de los cuerpos sólidos.
4.3. Relación entre el campo gravitónico y el gravitatorio.
Hasta aquí hemos explicado que el campo gravitatorio y el campo gravitónico tienen
ambos su causa en el gradiente de densidad del éter, pero al mismo tiempo hemos visto
que el gradiente obedece a una ley diferente en cada uno de estos campos.
También hemos visto cómo el campo gravitónico tiene efecto a pequeñas distancias
alrededor de las partículas de masa compacta que tienen un tamaño muy pequeño,
mientras que el campo gravitatorio tiene efecto a partir de grandes masas compuestas de
numerosas partículas compactas, lo que nos lleva a pensar que el campo gravitatorio se
crea a partir del campo gravitónico.
Hemos definido la masa compacta como una materia compuesta de electrinos que están
en contacto directo entre sí sin dejar espacios huecos en los que pueda penetrar el éter,
mientras la materia ordinaria, constituida por átomos, sabemos que está compuesta de
partículas subatómicas con separación entre sí que puede ser cien mil veces mayor que
dichas partículas.
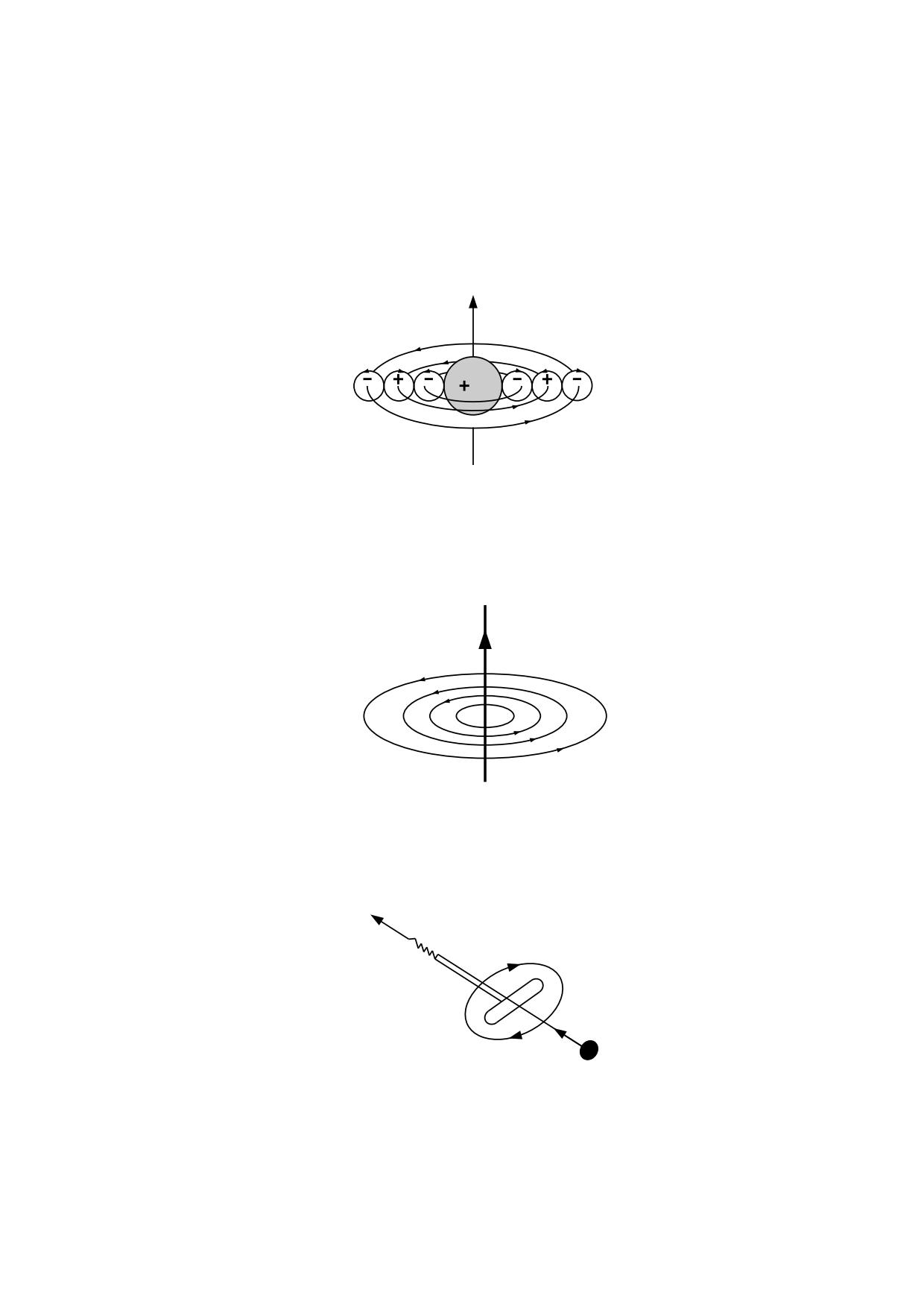
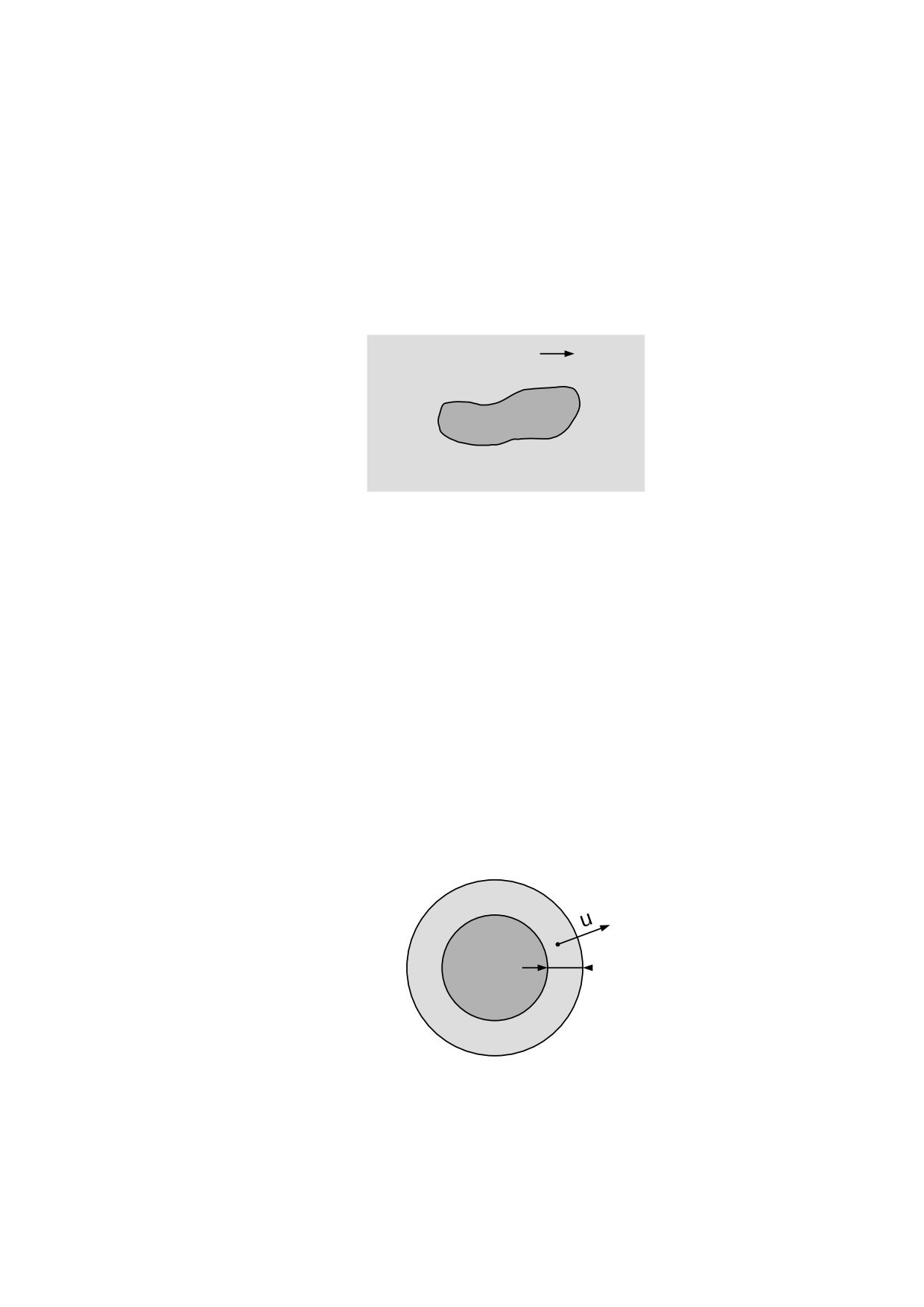
Consideremos la fig. 4.3.1 que es la representación simplificada de una esfera de materia
ordinaria compuesta de numerosas partículas de masa compacta.
Alrededor de cada partícula se originará un campo gravitónico que tendrá una distribución
radial de los eterones, tal como se muestra en la fig. 4.2.1, pero esta distribución radial se
combinará con las originadas por las otras partículas, quedando destruida y dando origen
al campo gravitatorio que ya conocemos y que depende de la masa total de las partículas
contenidas en la materia ordinaria.
fig. 4.3.1
Hasta ahora siempre que hemos tratado con la masa compacta hemos dedicado nuestra
atención a las partículas subatómicas, pero hemos de advertir que puede haber materia
compacta a escala astronómica, como pueden ser las estrellas de neutrones, los agujeros
negros y otros.
En estos casos, alrededor de estos cuerpos se creará un campo gravitónico, tal como el
que hemos estudiado para las pequeñas partículas de masa compacta. Las leyes deberán
ser las mismas cualquiera que sea el tamaño, siempre que las condiciones sean
equivalentes.
Si toda la masa del universo se reuniera en una esfera de masa compacta, solo habría
campo gravitónico alrededor de la misma, siempre que hubiera éter para sustentarlo.
4.4. Densidad del éter interior.
Denominamos éter interior al éter que ocupa el espacio libre existente entre las partículas
subatómicas que constituyen un cuerpo de cualquier sustancia.
La densidad del éter interior está condicionada por la densidad básica del éter en la zona y por la
presencia de las partículas de masa compacta propias del material, de acuerdo con la ecuación 4.2.3
que dice:
mK3
ρ=ρb+
r3
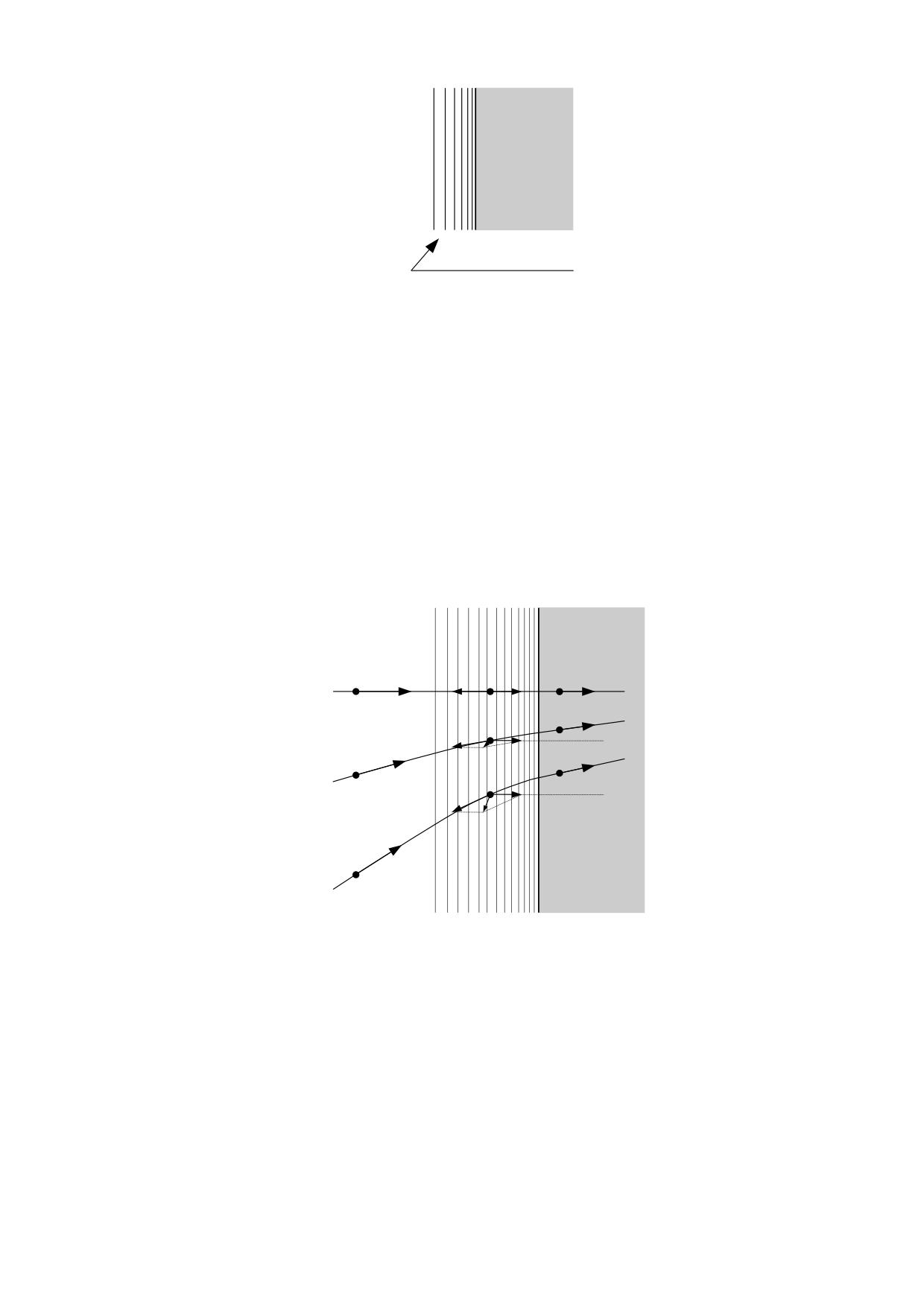
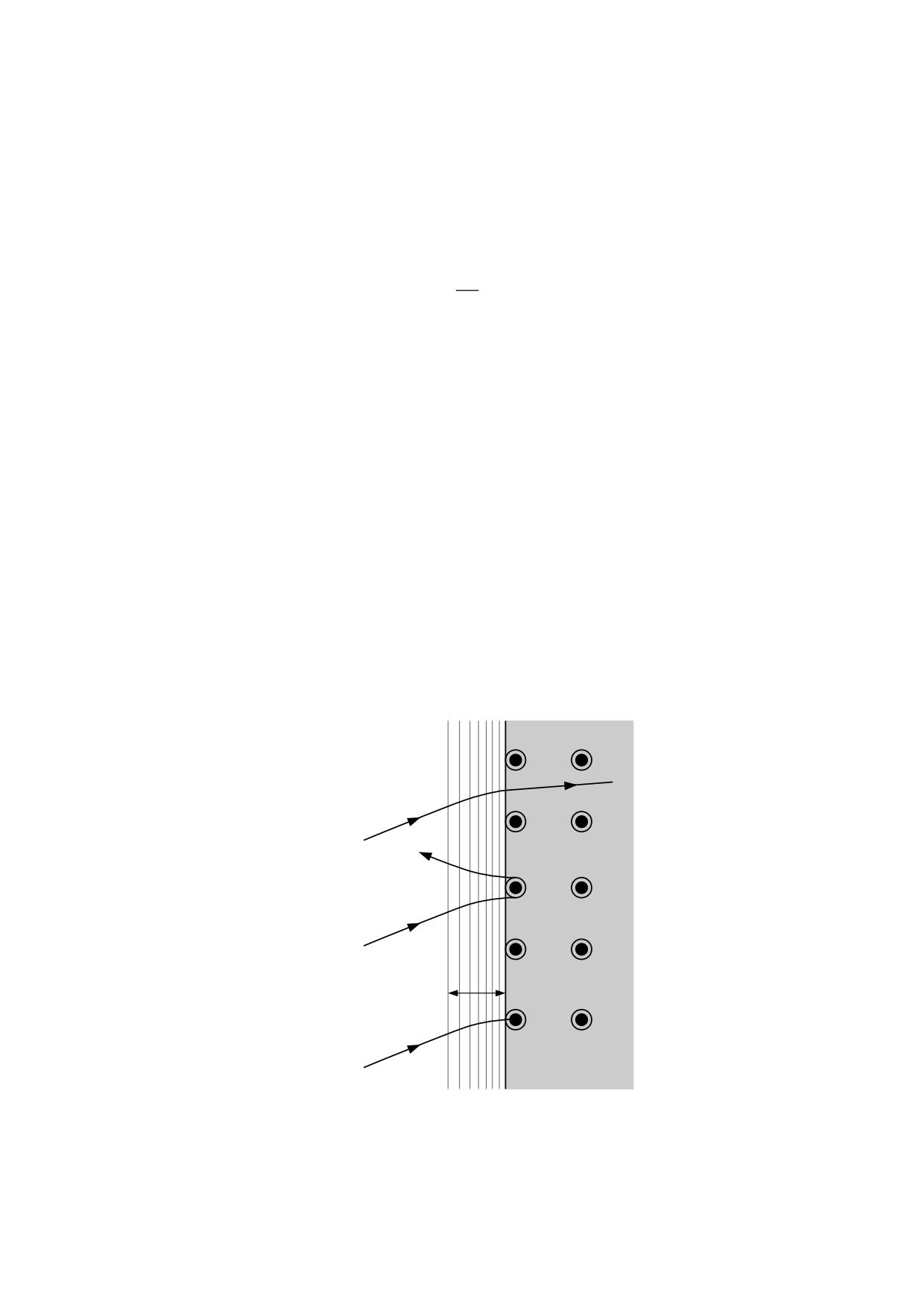
La propagación de la luz demuestra que la densidad media del éter en el interior de un
vidrio o del agua, alcanza un valor que es aproximadamente el doble del que tiene el éter
de nuestro entorno, al que denominaremos nuestro éter ambiental, designándolo ρa.
Debido a que los cuerpos transparentes tienen una composición muy variada y además la
distribución de las partículas en el espacio también difiere entre unas sustancias y otras,
no se puede determinar de modo sencillo la relación que existe entre la densidad
específica del material y la densidad del éter interior, pero es un hecho comprobado que
generalmente a una mayor densidad del material le corresponde un índice de refracción
más elevado, lo cual denota una mayor densidad del éter interior.
También se puede comprobar que al aumentar la presión de un gas aumenta su índice de
refracción, debido a que hemos incrementado su densidad.
Los fenómenos de espejismo que se observan algunas veces en nuestra atmósfera se
explican por la diferencia de densidad que se produce en las capas de aire cuando está
en reposo y por efecto del calor del suelo, al dilatar las capas más bajas.
El éter, contrariamente a la idea que se tenía en el siglo XIX, no está fijo en el espacio, lo
cual no tiene ninguna razón lógica si no se define respecto a qué cosa está fijo, ya que si
se considera la relatividad del movimiento es necesario establecer una referencia para el
mismo.
La realidad es que el éter está condicionado por la presencia de las masas, alrededor de
las cuales se concentra y además participa de su movimiento de acuerdo con unas leyes
que vamos a deducir seguidamente.
Si en el universo solo existiera un núcleo de masa rodeada de una nube de éter, esta
nube sería arrastrada por el núcleo de masa y la acompañaría en su movimiento.
En este caso imaginario, al no haber otras masas en el espacio, el incremento de
densidad provocado por la masa única, resultaría ser la densidad absoluta del éter.
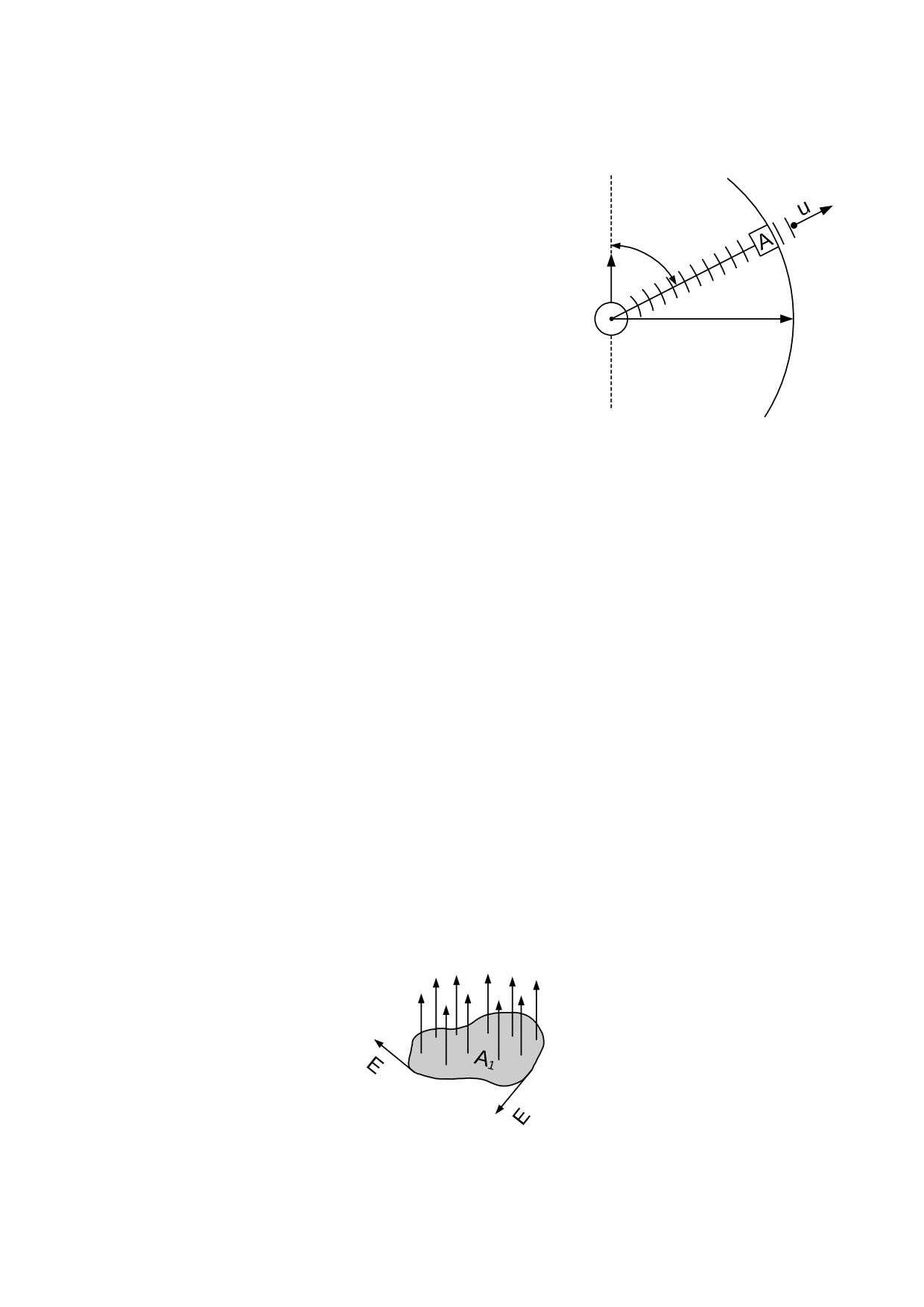
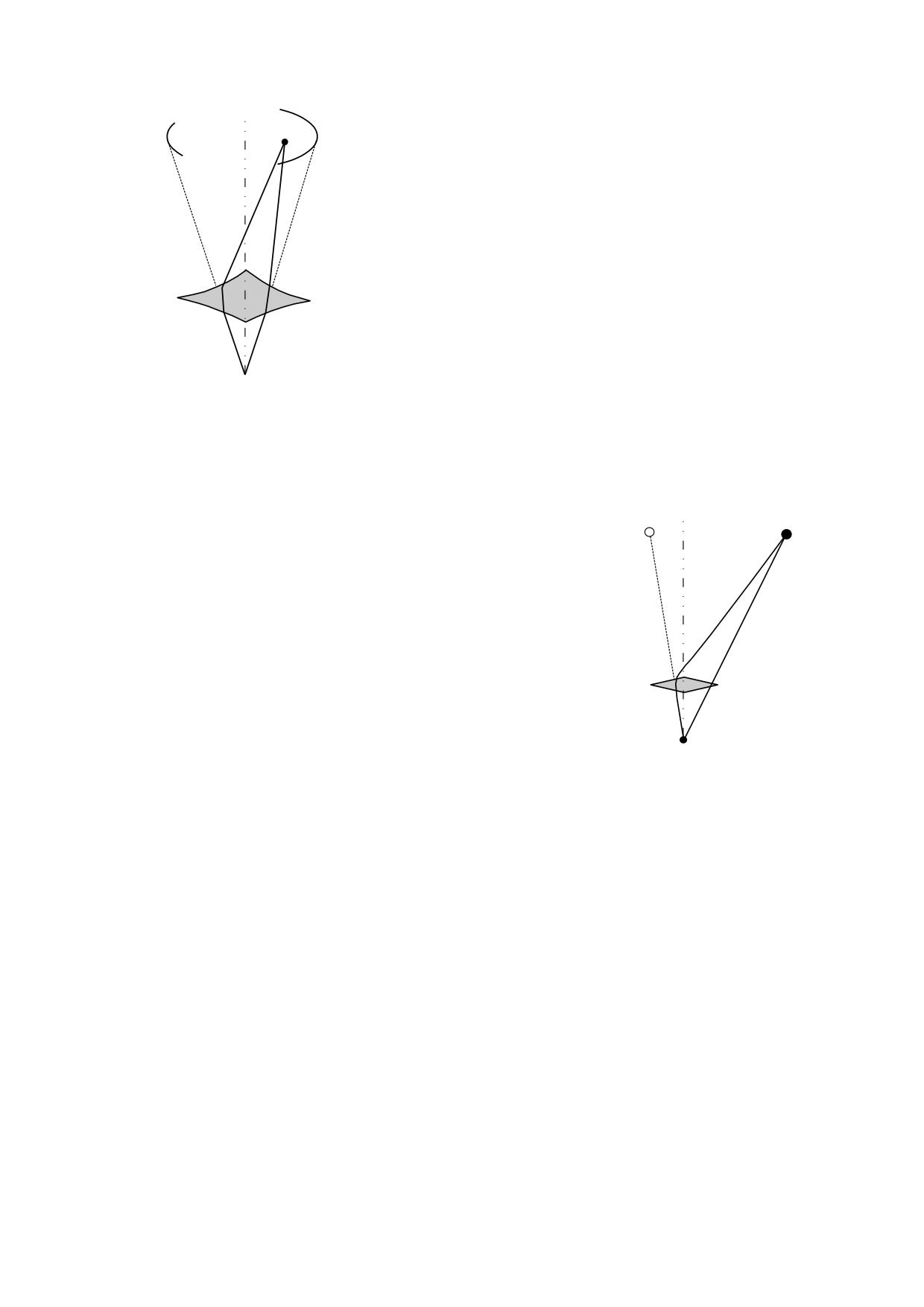
Ahora imaginemos dos únicos núcleos de masa y
m1
v1
tomamos uno de ellos como referencia del movimiento, tal
como se representa en la fig. 4.5.1. La masa m1 se
desplaza con la velocidad v1 respecto a la masa m0 que
r1
consideramos en reposo.
P
v
La densidad del éter en un punto cualquiera dependerá de
m1 y m0.
r
0
ρ =Δρ0+Δρ1
V = 0
fig. 4.5.1
m0
Consideremos ahora un volumen de éter situado en el punto P. La masa de este volumen
de éter será proporcional a la densidad del mismo:
me=Vρ=V (Δρ0+Δρ1)
Esta masa de éter participa de ∆ρ con velocidad v1 y de ∆ρ0 en reposo.
Aplicado el principio de la conservación de la cantidad de movimiento, que nos dice que el
producto mv debe ser constante, tendremos:
Vρ1v1=V (Δρ0+Δρ1)va
Δρ1 v1=( Δρ0 +Δρ1) va
donde va es la velocidad de arrastre resultante para la masa de éter me y cuyo valor
despejamos:
Δρ1
Δρ1
va=v1
va=v1
(4.5.1)
Δρo+Δρ1
ρ
En el universo real, la densidad básica del éter en cada región está condicionada por la
distribución de masas en el espacio sideral. Ahora vamos a considerar el arrastre del éter
tomando como referencia del movimiento el éter de nuestro ambiente y cuya densidad la
designaremos ρa, prescindiendo de las masas que han determinado esta densidad.
La presencia de una masa en movimiento alterará la densidad del éter y además
provocará un arrastre parcial.
En cualquier punto alrededor de la masa resultará una densidad del éter que valdrá
ρ=ρa + ∆ρ , con independencia de la ley que rige el incremento, que puede ser de campo
gravitatorio o gravitónico.
De acuerdo con la ecuación 4.5.1, la velocidad de arrastre es:
Δρ1
Δρ
va=v1
que en nuestro caso:
va=vm
(4.5.1)
ρ
ρa+Δρ
Esta ecuación es válida para un campo gravitatorio o para un campo gravitónico,
sustituyendo el valor de ∆ρ por el valor resultante de la aplicación de la ley
correspondiente a cada tipo de campo.
La validez de esta ley quedará demostrada al tratar el arrastre de la luz en el capítulo 10.
En el caso de un campo gravitatorio sabemos que:
Por lo tanto, a una distancia r desde la masa móvil, resultará una velocidad de arrastre
que será:
mK2
vmmK2
r
va=vm
va=
(4.5.3)
mK2
ρar+mK2
ρa+
r
Podemos observar que si hacemos que ρa tenga valor nulo en la ecuación 4.5.3, la
velocidad de arrastre va resulta igual a la velocidad de la masa vm, tal como se había
propuesto en el caso imaginario de una masa única en el universo.
Cuando participan en el fenómeno del arrastre varias masas con diversas velocidades y
direcciones, la velocidad resultante será la suma vectorial de los resultados parciales.
En el dominio de un campo gravitónico el incremento de densidad del éter será:
mK3
Δρ=
r3
Por consiguiente la velocidad de arrastre será:
(4.5.4)
En las distancias muy pequeñas ρa será muy reducida frente al término
lo cual
significa que la velocidad de arrastre en la superficie de las partículas se aproximará
mucho a la velocidad propia de la partícula.
5.1. Desplazamiento dieléctrico del éter.
La propiedad dieléctrica del éter nos proporciona la posibilidad de explicar el fenómeno de
los campos de fuerza eléctricos, demostrando al mismo tiempo que es la fuerza
coeléctrica de contacto la que origina la fuerza eléctrica que se manifiesta a distancia.
En la descripción del éter proponíamos que estaba compuesto de eterones con cargas
eléctricas positivas unos y con cargas negativas otros, dispuestos alternativamente.
La carga eléctrica de los eterones puede desequilibrase sobre los mismos, ya sea por una
alteración de su densidad, o bien por una variación en su forma. Su característica de
elasticidad ya ha quedado demostrada al explicar el campo gravitatorio.
Recordemos de nuevo que en el vacío absoluto no se produce ningún efecto de fuerza y
por consiguiente deberemos considerar únicamente las fuerzas que se producen por el
contacto directo.
Las fuerzas coeléctricas producidas por el contacto de un cuerpo con carga eléctrica neta
y el éter que sufre un desplazamiento dieléctrico, son las causantes de la fuerza eléctrica
que aparentemente se produce a distancia, lo cual demostraremos después de explicar la
naturaleza del campo eléctrico.
Un campo eléctrico puede ser definido como un espacio en el cual el éter sufre un
desplazamiento dieléctrico provocado por la presencia de un cuerpo con carga eléctrica
neta.
En la fig. 5.1.1 se representa el desplazamiento de la carga eléctrica de los eterones
causado por una superficie que tiene carga neta positiva.
+
--+ -++ --+
-++
-
-
+
-++ - +
-++
- +
q1
+
--+ -++ --+ -++
-
-
+
fig. 5.1.1
-++ - +
-++
- +
La cantidad de carga desplazada a través del éter es igual a la carga neta inductora
presente en la superficie del cuerpo y permanece constante aunque se extienda en el
espacio abarcando superficies cada vez mayores. Esto tiene como consecuencia que la
densidad de carga superficial resulte inversamente proporcional a la superficie abarcada:
q
σ=
(5.1.1)
A
En el caso de una superficie esférica la densidad de carga superficial resultará:
q
σ=
(5.1.2)
4 πr2
Cuando el cuerpo inductor es muy pequeño respecto a la superficie considerada, se
puede tratar a la carga inductora como si fuera una carga puntual o una carga esférica,
aunque tenga una forma cualquiera.
La física clásica ha definido la intensidad de campo eléctrico en relación con la distancia
desde una carga puntual. En el espacio vacío y utilizando el sistema de unidades c.g.s.
electrostáticas, la magnitud de la intensidad del campo eléctrico queda definida por la
siguiente ecuación:
q
E=
u.e.s en c.g.s
r2
Como la superficie esférica es A=4πr2, podemos expresar la intensidad de campo
eléctrico en función de la superficie abarcada, de modo que resulta:
4πq
E=
(5.1.3)
A
Como la densidad de carga superficial obedece a la ecuación 5.1.1 podemos también
expresar:
E=4 πσ
(5.1.4)
5.2. La fuerza eléctrica.
Cuando un cuerpo con carga eléctrica neta está inmerso en un campo eléctrico, surge
una fuerza causada por el desequilibrio de las fuerzas coeléctricas que se producen en la
superficie de contacto con el éter. Pero si queremos determinar la magnitud de esta
fuerza, será necesario analizar antes el comportamiento de estas fuerzas cuando la
superficie de contacto tiene acumulada una carga eléctrica.
Ya sabemos que en el contacto absoluto se produce una fuerza de cohesión, aunque los
cuerpos no tengan carga eléctrica neta, que conocemos como fuerza coeléctrica y
obedece a la ecuación 2.3.1:
F=ρ1ρ2 AK1
En esta ecuación ρ expresa la densidad de masa de los elementos en contacto, por lo
cual nos ha sido útil en el caso de los campos gravitatorios que dependen directamente
de la masa. Sin embargo ahora necesitamos aplicarla al caso de las fuerzas eléctricas
que dependen de la carga eléctrica neta, por lo cual será necesario sustituir la densidad
de masa por la densidad de carga eléctrica correspondiente.
Además deberemos asumir que la carga eléctrica de los electrinos que constituyen
cualquier material es proporcional a su masa por lo que introducimos un factor de
proporcionalidad K4, de modo que:
q=K4m
(5.2.1)
Por consiguiente, la densidad de carga, que designaremos con la letra δ resultará:
δ
δ=K4 ρ y ρ=
K4
Sustituyendo en la ecuación 2.3.1 la densidad de masa por la densidad de carga eléctrica,
la fuerza queda determinada por:
δ1δ2 AK1
F=
(5.2.2)
2
K
4
En la ecuación 5.2.2 la letra δ significa una densidad por volumen de la carga eléctrica,
que no debemos confundir con la densidad de carga superficial que se ha designado con
la letra σ. Por lo tanto deberemos determinar el valor de δ que resulte para la carga
superficial de una partícula.
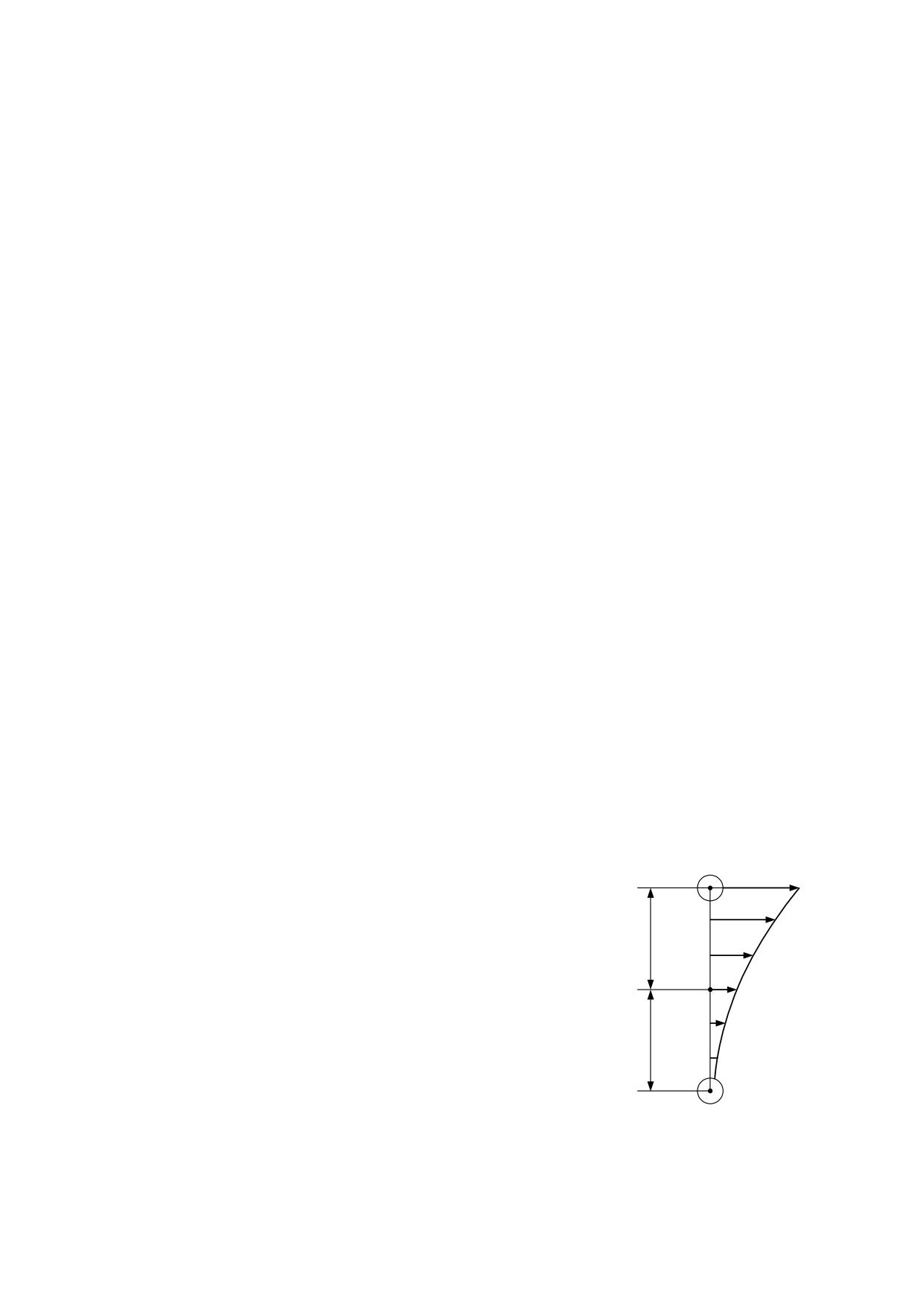
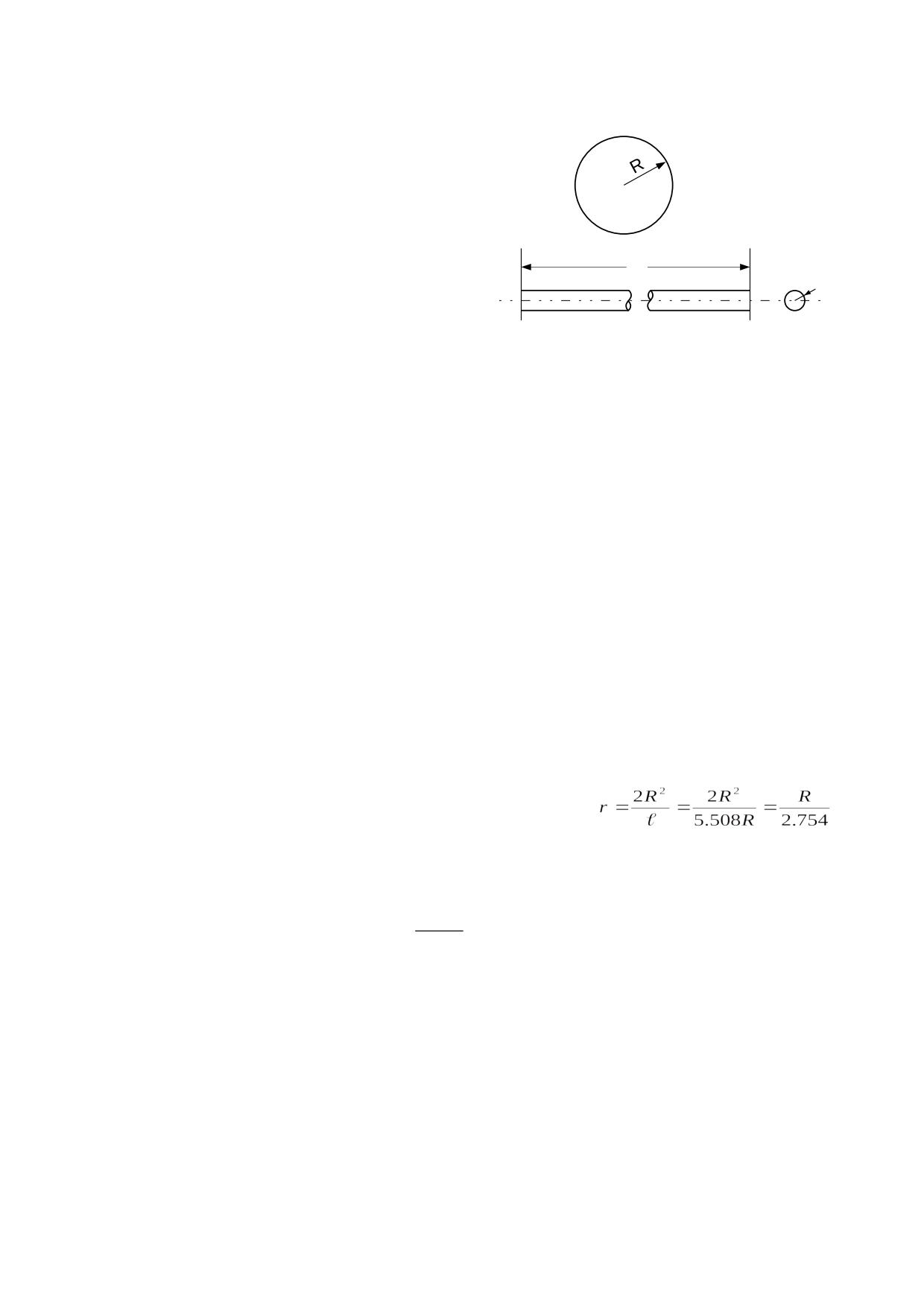
Cuando una partícula tiene una carga eléctrica neta, esta carga consiste en una cantidad
de electrinos que se sitúan en la superficie y ocupa un espesor (D) que corresponde al
diámetro de los electrinos, tal como se representa en la fig. 5.2.1. Este espesor tiene una
dimensión constante, pues las partículas no pueden retener sobre su superficie más de
una capa de electrinos.
r
fig. 5.2.1
Con independencia de cual sea la forma de la partícula, ésta tendrá una superficie con un
área que designamos con la letra A.
Podemos asumir que los electrinos tienen un diámetro muy pequeño en relación al
tamaño de la partícula, por lo cual podemos determinar de forma muy sencilla el volumen
de la corteza ocupada, que resultará:
V = AD
A = superficie
y D = espesor
q
La densidad de carga eléctrica por volumen es:
δ=
V
q
Por consiguiente:
δ=
AD
Llevando este valor de δ a la ecuación 5.2.2 tendremos:
q1 q2 K1
F=
(5.2.3)
2
AD2
K
4
Los factores K1, D2 y K42 son cantidades constantes, lo que nos permite reunirlos en un
solo factor:
K1
=K
(5.2.4)
2
D2K
4
Sustituyendo esta equivalencia en la ecuación 5.2.3 obtenemos:
q1q2
K
F=
(5.2.5)
A
donde K es un factor de proporcionalidad.
Una vez determinada la fuerza producida entre las cargas superficiales de signo opuesto
pasaremos a analizar el efecto producido por el desplazamiento dieléctrico del éter sobre
una partícula con carga eléctrica neta.
Cuando una partícula sin carga neta está inmersa en un campo eléctrico quedará
sometida a fuerzas coeléctricas en toda su superficie, pero la magnitud y el sentido de
estas fuerzas es tal que la suma vectorial resultará nula. Sin embargo cuando la partícula
tiene una carga eléctrica neta, el equilibrio de fuerzas no es posible, porque en la zona
donde la carga desplazada en el éter es de signo opuesto a la carga de la partícula, se
producirá una fuerza mayor que en la zona en la cual el signo de las cargas es
coincidente.
F
q
fig. 5.2.3
E
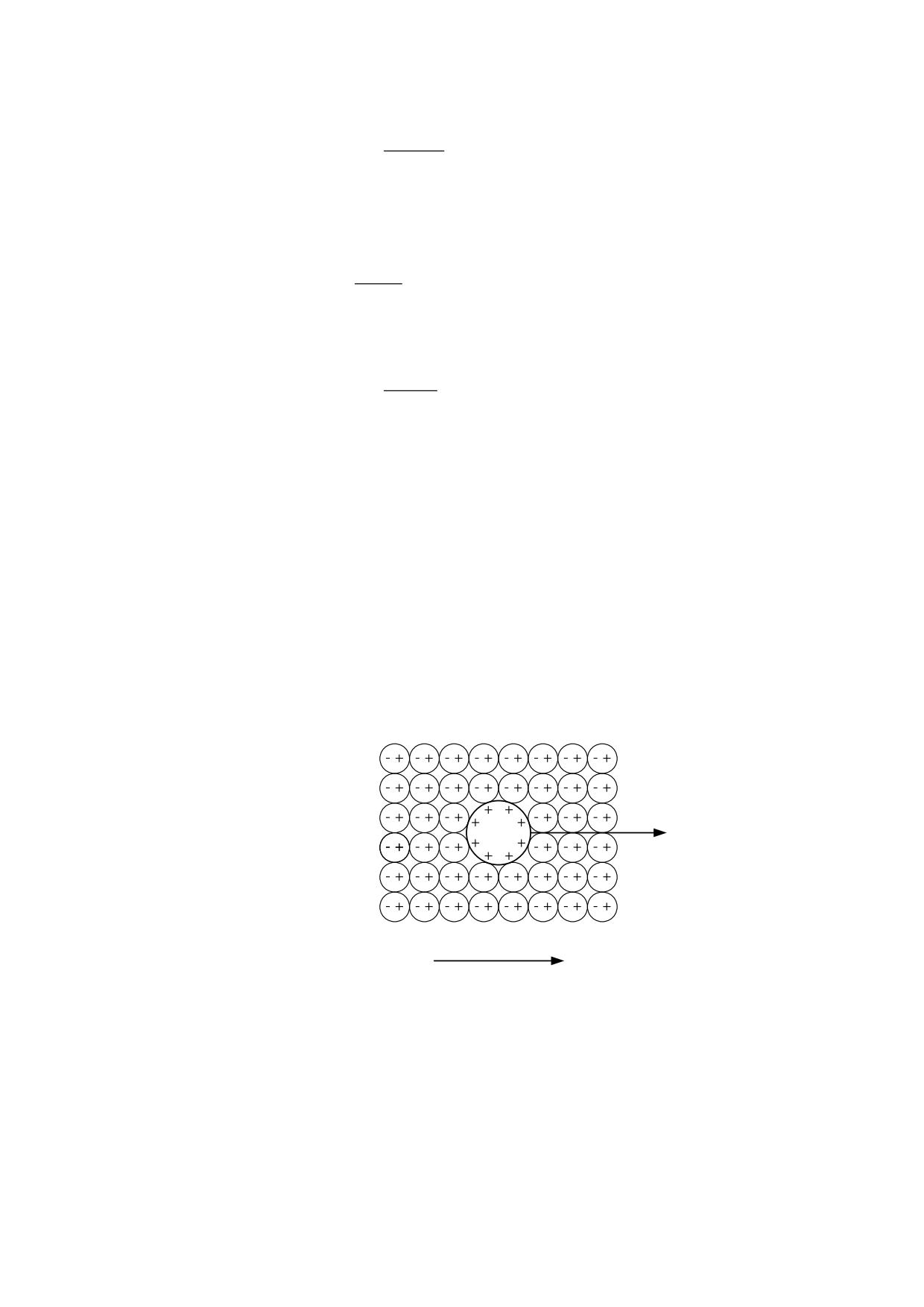
En la figura 5.2.3 se representa de forma simplificada la posición de las cargas
desplazadas en los eterones con relación a la partícula que tiene carga positiva neta.
Deberemos entender que el número de eterones que intervienen en un caso real será
muchísimo mayor que los representados en esta figura.
Si en la figura 5.2.3. la carga de la partícula tuviera signo negativo, la fuerza resultante
tendría sentido inverso al representado, por lo tanto contrario al sentido del campo
eléctrico E.
Para adaptar la ecuación 5.2.5 a las circunstancias de un campo eléctrico a la carga q1 la
denominaremos carga desplazada y la designaremos qd, de modo que la ecuación será
ahora:
qd q2 K
F=
(5.2.6)
A2
Donde A2 es el área de la proyección de la partícula sobre un plano perpendicular a la
dirección del campo eléctrico.
Ahora podemos determinar el valor de la fuerza ejercida sobre una carga situada en el
campo eléctrico originado por una carga puntual, cuya intensidad obedece a la ecuación
5.1.3 y que nos dice:
4πq1
E=
A1
La carga desplazada sobre el área A2 será:
4 πq1 A2
qd=EA2
qd=
A1
Sustituyendo este valor en la ecuación 5.2.6 tendremos:
4 π Kq1q2
F=
A1
Pero A1 es la superficie esférica que vale 4πr2, por lo cual tendremos:
4 π Kq1q2
Kq1 q2
F=
F=
(5.2.7)
4 πr2
r2
Dando al factor K el valor unidad, tendremos:
q1q2
F=
u.e.s.
(5.2.8)
r2
Esta ecuación expresa la conocida ley de Coulomb, a la cual hemos llegado a partir de la
ley de la fuerza coeléctrica, demostrando así que la fuerza eléctrica a distancia se
produce debido al contacto con el éter, cuando éste está sometido a un desplazamiento
dieléctrico.
El hecho de que el factor de proporcionalidad K sea la unidad no es una casualidad, pues
se debe a que la unidad de carga eléctrica en el sistema de medidas electrostáticas c.g.s.
fue dimensionada para que en la ecuación 5.2.8 resultase una fuerza de una DINA a una
distancia de un centímetro, lo cual determina que el factor K sea la unidad cuando la
ecuación 5.2.7 se expresa en unidades electrostáticas c.g.s.
5.3. Sentido de la fuerza eléctrica.
A diferencia del campo gravitatorio, en el cual la fuerza siempre tiene el mismo sentido de
acuerdo con el gradiente de densidad del éter, en el campo eléctrico el sentido de la
fuerza depende del sentido del campo y además del signo de la carga eléctrica.
Un campo eléctrico se puede representar vectorialmente y se ha convenido en que su
sentido esté orientado desde la carga positiva hacia la carga negativa.
E
F
F
fig. 5.3.1
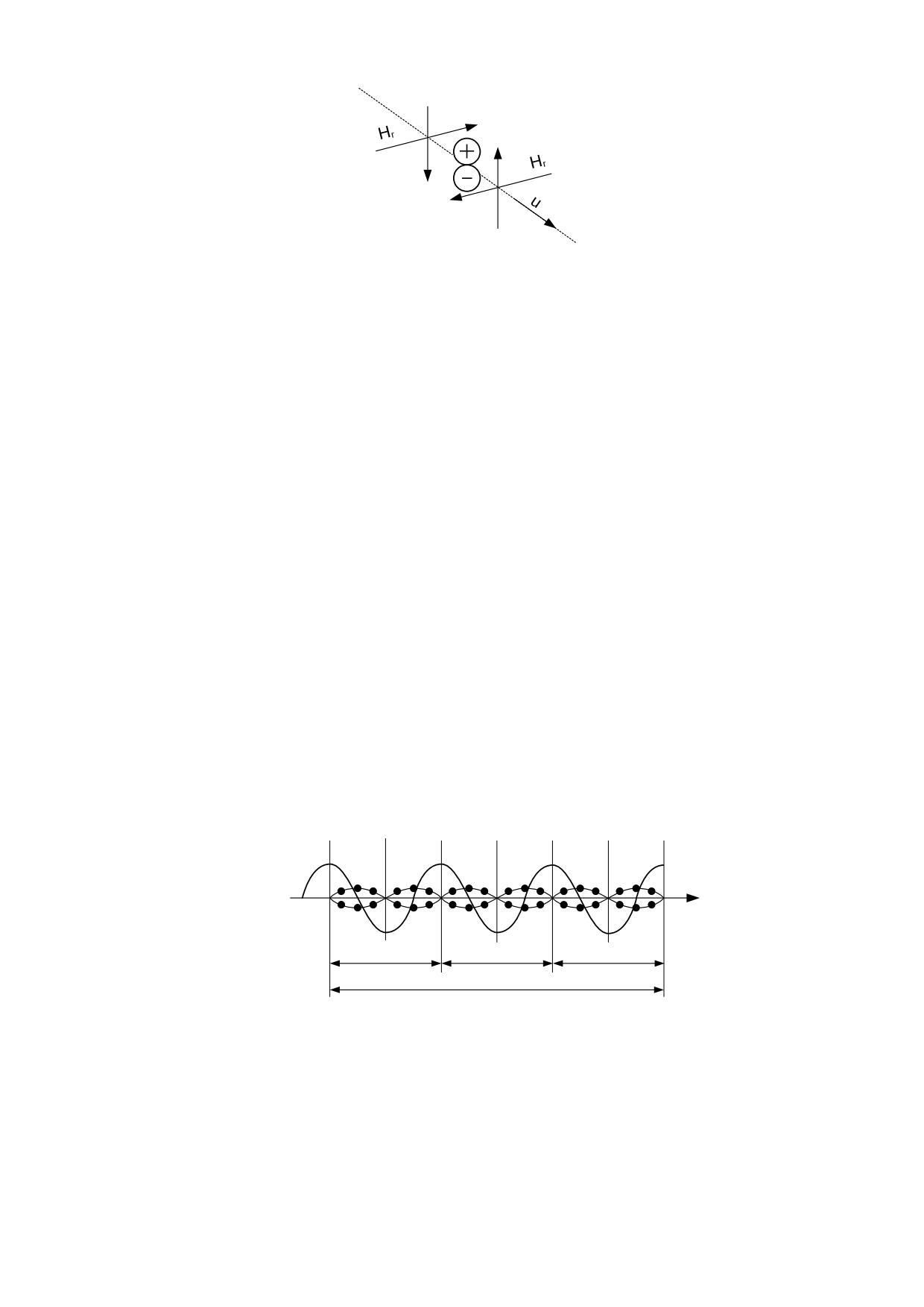
En la figura 5.3.1 se representa una carga en reposo que genera un campo eléctrico y las
fuerzas que resultan sobre dos cargas de signos diferentes.
Si alguna de las cargas está en movimiento respecto al éter, el sentido de la fuerza ya no
estará dirigido desde una carga hacia otra, porque el campo eléctrico necesita un tiempo
para propagarse y durante ese tiempo la carga en movimiento habrá recorrido un camino
hasta otra posición.
El éter siempre será la referencia del movimiento de cualquier cuerpo o partícula, lo
mismo en los fenómenos eléctricos como en los gravitatorios.
5.4. Efecto de los materiales dieléctricos.
La experiencia demuestra que los materiales dieléctricos hacen que disminuya el campo
eléctrico en un factor específico de cada sustancia, al cual se le conoce como constante
dieléctrica del material. Este comportamiento se explica del modo siguiente: en los
cuerpos aislantes, el campo eléctrico provoca un desplazamiento relativo entre las cargas
positivas y negativas que constituyen el material, ya sean moléculas polares o
simplemente protones y electrones. Este desplazamiento tiene que vencer las fuerzas que
mantienen el equilibrio de la estructura del material, originando al mismo tiempo un campo
eléctrico de sentido contrario al campo sustentado por el éter, de modo que este queda
disminuido.
Ed
E
q/2
q/2
Eo
fig. 5.4.1
Consideremos la fig. 5.4.1 en la cual se provoca un campo eléctrico por la carga
acumulada en dos placas paralelas.
En ausencia del material dieléctrico se producirá un campo eléctrico cuya intensidad será:
4 πq
Eo=
A
Al intercalar entre las dos placas un material dieléctrico, se produce en el seno del mismo
un desplazamiento de las cargas que lo constituyen, originando un campo de reacción Ed
que tiene sentido contrario a Eo.
4 πqd
Ed=
de modo que
E = Eo-Ed
A
La relación
es conocida como la constante dieléctrica del material, por consiguiente:
Eo
Eo
Kd=
y
E=
E
Kd
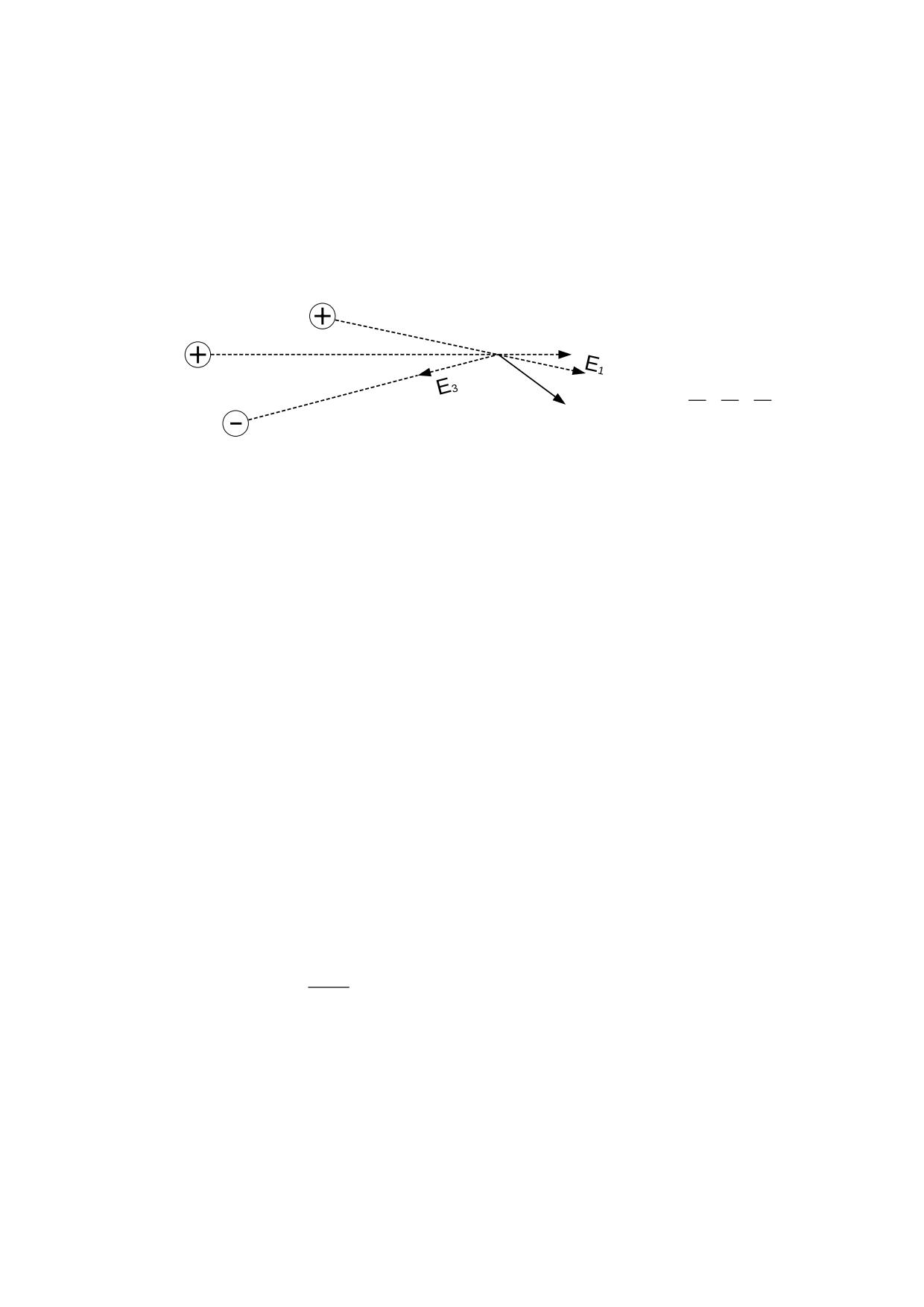
5.5. Suma de campos eléctricos.
Cuando el desplazamiento dieléctrico del éter es producido por diversas cargas
separadas, que además pueden tener distintos signos, el campo resultante en un lugar
determinado será la suma vectorial de los campos producidos por cada una de las cargas.
La fig. 5.5.1 ilustra este caso.
q1
E=E
+E2+E3
1
q2
E
2
q1
q2
q3
q
3
E=
+
+
2
E
r
r2
r2
1
fig. 5.5.1
Esta ley postula que el flujo neto a través de una superficie que encierra un conjunto de
cargas eléctricas, es igual al producto de la carga neta por 4π:
Φ=4 πqn
(5.6.1)
De acuerdo con los conceptos de esta teoría del éter, se puede enunciar del siguiente
modo:
La carga neta desplazada en el éter sobre una superficie que encierra un conjunto de
cargas eléctricas es igual a la carga neta contenida (ver sección 5.1).
qd=qn
(5.6.2)
Esta equivalencia se demuestra porque:
4 πqd
E=
luego
Φ=EA=4 πqd
A
5.7. Energía almacenada en un campo eléctrico.
La física clásica demuestra que la energía almacenada en un campo eléctrico con un
volumen V tienen una magnitud que es:
E2V
U =
8π
La física del éter explica este resultado como el efecto del desplazamiento de la carga de
los eterones venciendo una fuerza elástica. El campo eléctrico equivale a un muelle
distendido, tal como veremos seguidamente:
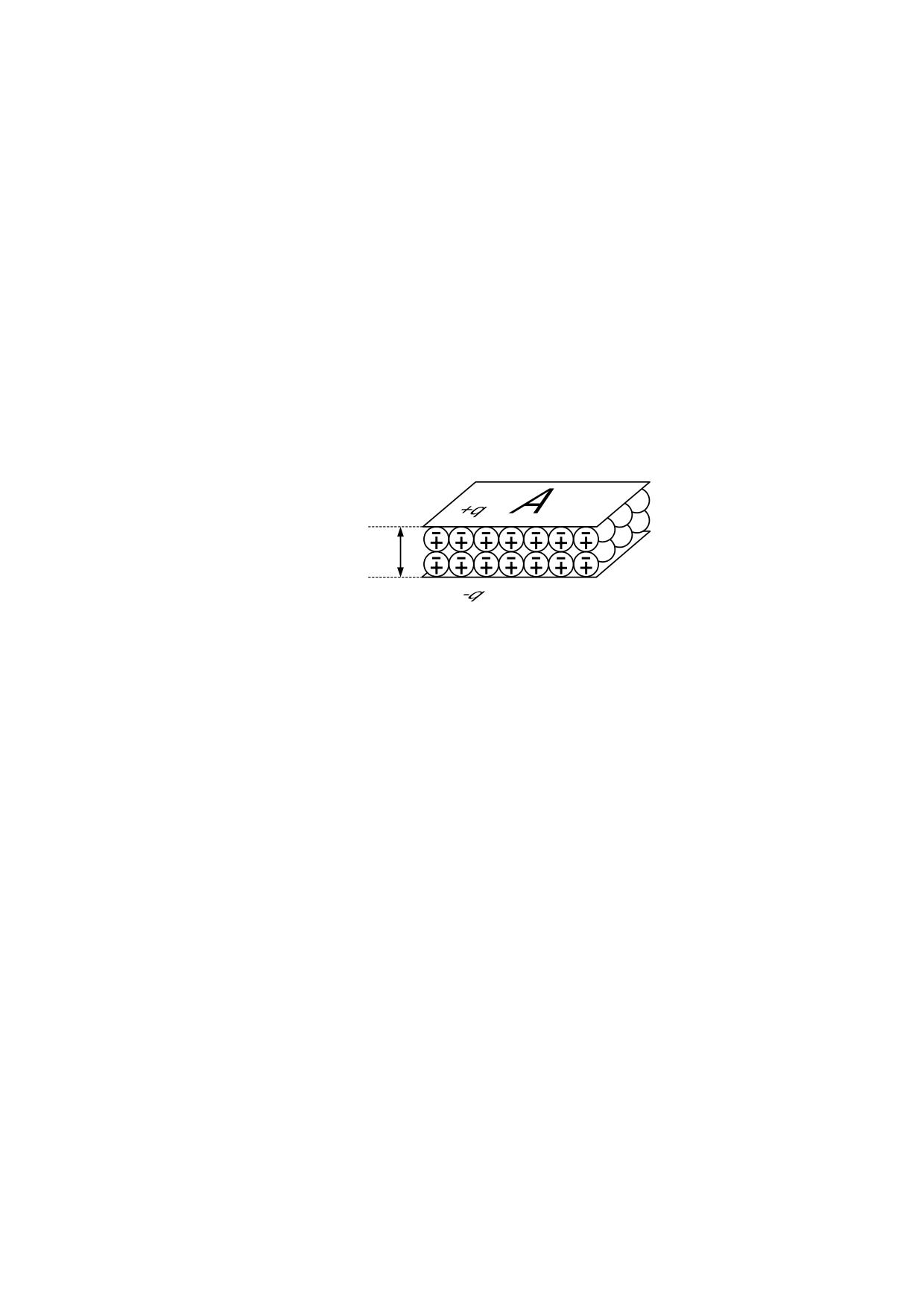
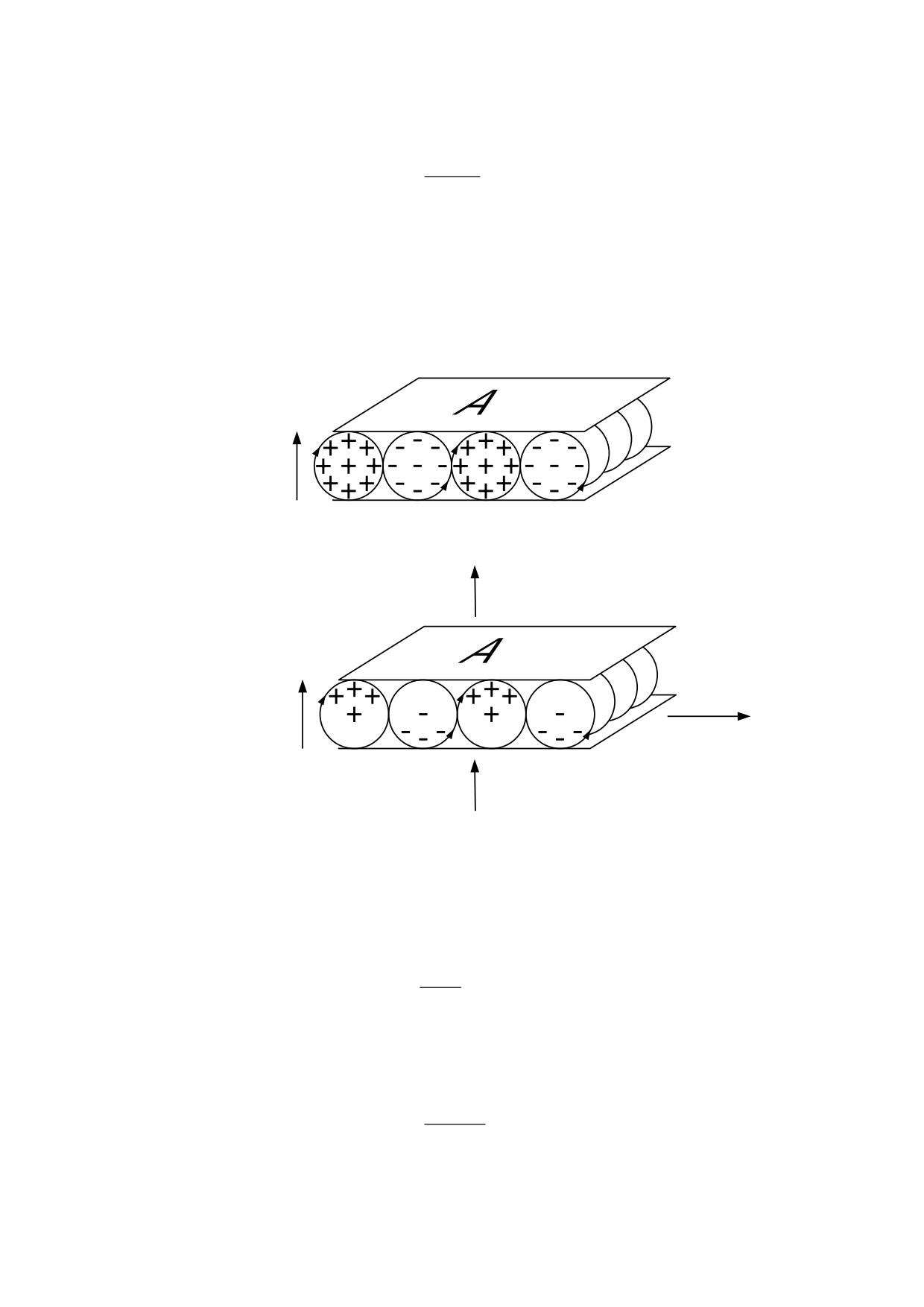
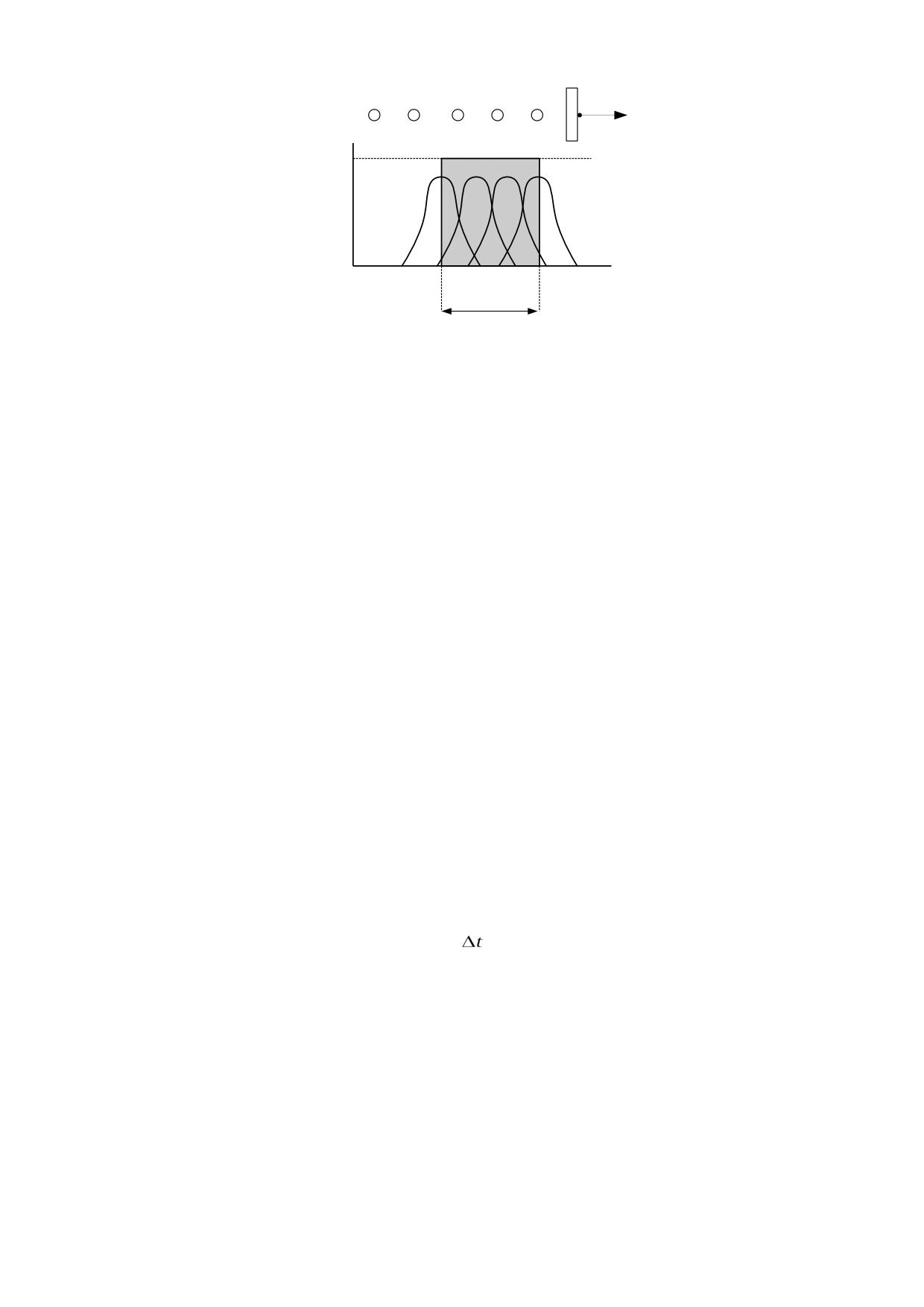
Si disponemos dos placas conductoras en posición paralela, tal como indica la figura 5.7.1
con una separación d que resulte despreciable respecto a la superficie A y cargamos
ambas placas con cargas iguales de signos opuestos, obtendremos un campo eléctrico
uniforme contenido entre las mismas.
d
fig. 5.7.1
La carga eléctrica de los eterones sufrirá un desplazamiento venciendo la fuerza elástica
de los mismos y originando un campo E cuyo valor será:
4 πq
8 πq
EA
E=2 x
=
donde
q=
A
A
8π
Sobre cada placa se ejercerá una fuerza de valor F=Eq, por consiguiente:
E2 A
F=
8π
Si ahora permitimos que una de las placas se desplace bajo la acción de esta fuerza,
recorrerá la distancia d hasta la otra placa. Por lo tanto producirá un trabajo cuya
magnitud será: W=Fd
E2 Ad
W = Fd =
pero
Ad= volumen entre placas=V
8π
E2V
por consiguiente: W=
, producido por la energía almacenada
8π
E2V
W=U
luego
U=
(5.7.1)
8π
Los resultados de aplicar los nuevos conceptos, que se apoyan en la existencia de un éter
dieléctrico, están en total conformidad con la electrostática clásica, si exceptuamos el
nuevo concepto que niega la repulsión intrínseca de las cargas eléctricas en contacto
absoluto.
Resulta innecesario extenderse en la explicación de otros fenómenos tales como el
potencial eléctrico, la capacidad, etc., pues no haríamos otra cosa que repetir
demostraciones sobradamente conocidas.
El hecho de que no exista la repulsión eléctrica intrínseca entre cargas del mismo signo
no cambia nada en las leyes de la electrostática mientras no se trate de los fenómenos
que ocurren en el interior de los núcleos atómicos, pero en este caso la importancia de
este principio es fundamental.
Con el fin de conseguir la máxima sencillez en las ecuaciones que expresan las leyes de
electricidad y del magnetismo, hemos adoptado el sistema de unidades c.g.s. que permite
eliminar algunos factores de proporcionalidad.
La física clásica nos presenta la fuerza magnética como un fenómeno relacionado con la
corriente eléctrica y nos proporciona las leyes que nos permiten calcular su magnitud,
pero hasta ahora no se ha podido dar una explicación de esta fuerza que se produce
aparentemente a distancia.
La existencia del éter nos va a permitir explicar la fuerza magnética como una fuerza
producida por el contacto con el éter, cuando los eterones que lo constituyen están
sometidos a un movimiento de rotación.
Asimismo el éter nos proporcionará una explicación de la naturaleza de las ondas
electromagnéticas y del fenómeno de la inducción electromagnética.
Para seguir esta demostración deberemos rechazar de nuestra mente la idea de campo
de fuerza en el vacío a lo cual estamos acostumbrados y que surgirá con insistencia
siempre que tengamos que imaginar un campo de fuerza.
Una de las características peculiares del campo magnético que lo distingue de todos los
demás, es el hecho de que este campo no ejerce ninguna fuerza sobre partículas
inmóviles respecto al mismo campo. Otra característica especial es que la fuerza
resultante sobre una carga eléctrica en movimiento tiene siempre un sentido
perpendicular a la trayectoria de la carga, aunque la dirección de esta trayectoria cambie
respecto al campo.
Este comportamiento tan especial es un valioso indicio para llegar a la conclusión de que
obedece al movimiento de rotación de los eterones, como será demostrado más adelante.
Es muy importante considerar que si la fuerza magnética siempre es perpendicular a la
trayectoria de la carga móvil, significa que es totalmente independiente de la posición
relativa de la otra carga que ha originado el campo.
6.2. Generación del campo magnético.
De acuerdo con la descripción del éter propuesta en la sección 2.1 éste se compone de
elementos esféricos que hemos llamado eterones, una mitad de los cuales tienen carga
eléctrica positiva y la otra mitad carga negativa.
Los eterones se distribuyen en el espacio de modo que solo entran en contacto los que
tienen signos opuestos, lo cual les obliga a ordenarse formando una red cúbica que les
permite girar sin producir ningún rozamiento.
Para originar un campo magnético bastará que una carga eléctrica de cualquier signo se
desplace a través del éter. Esta carga móvil solo tendrá cohesión con aquellos eterones
que estén en contacto directo y que además tengan signo opuesto.
La carga móvil hará girar a los eterones de signo opuesto y estos transmitirán el
movimiento giratorio a todos los demás, de modo que este movimiento se extenderá en el
éter circundante siguiendo unas leyes que estudiaremos más adelante.
V
fig. 6.2.1
En la fig. 6.2.1 se muestra un número pequeño de eterones para simplificar la imagen,
pero deberá entenderse que la cantidad de eterones en contacto con la carga puede
alcanzar un elevado número. También deberá considerarse que la trayectoria de la
partícula está en el plano del papel y por consiguiente el eje de rotación de los eterones
representados resultará perpendicular al mismo plano.
Se puede observar que en cada lado de la trayectoria resulta una rotación de sentido
opuesto para los eterones del mismo signo, lo cual determina que en el eje de la
trayectoria, la rotación queda anulada. Este hecho explica por qué la intensidad de campo
es máxima en el plano perpendicular a la trayectoria mientras resulta nula sobre la propia
trayectoria.
La explicación anterior está en conformidad con la
P
electrodinámica clásica, que nos dice que la intensidad
V
del campo magnético resultante en un punto cualquiera es
θ
proporcional al seno del ángulo formado por la trayectoria
y la línea recta que va desde dicho punto hasta la carga
móvil, según ser representa en la fig. 6.2.2. Cuando las
q
cargas eléctricas se mueven dentro de un conductor,
constituyendo una corriente eléctrica, la intensidad del
fig. 6.2.2
campo magnético será la suma del efecto producido por
todas las cargas que participan en dicha corriente.
El fenómeno se produce del mismo modo que en las cargas móviles aisladas, debido a
que el éter ocupa los espacios interatómicos del conductor en el cual se desplazan.
También se genera un campo magnético cuando en el éter se produce un desplazamiento
de cargas motivado por la variación del campo eléctrico, debido a la propiedad dieléctrica
del éter.
Este hecho que resulta inexplicable en el vacío, es un simple movimiento de cargas
cuando consideramos la existencia del éter. Este fenómeno es conocido como “corriente
de desplazamiento de Maxwell”.
Puede sorprender el hecho de que la velocidad de rotación de los eterones resulte
diferente en función de la distancia y de la posición relativa que ocupan, lo cual sería
imposible si los eterones fueran elementos rígidos, pero ya se ha explicado al definir los
eterones en la sección 2.2 que están dotados de elasticidad o compresibilidad, lo cual
permite que su velocidad se adapte a las condiciones del campo magnético que
trataremos más adelante.
La descripción dada inicialmente para explicar la generación del campo magnético ha sido
simplificada al omitir el efecto de arrastre que deberá producirse al desplazarse la carga
móvil, tal como ha sido explicado en la sección 4.5.
No obstante dicha explicación es perfectamente válida porque a pesar de producirse un
determinado arrastre, finalmente este arrastre tiende a extinguirse en una distancia muy
pequeña al ser producido por un campo gravitónico.
La velocidad tangencial de los eterones quedará reducida en el valor que tenga la
velocidad de arrastre, de modo que en cada eterón tendremos:
vT =vq-va
va→0
Cuando la velocidad de arrastre alcance un valor despreciable, la velocidad tangencial
será la misma que la de la partícula que origina el movimiento de rotación.
Va
0
Va1
Vq
Va2
Va3
Va4
Va5
Va6
q
fig. 6.2.3
VT1
VT2
VT3 VT4
VT5 VT6
Al estudiar el arrastre del éter por el movimiento de una masa pudimos ver que cuando el
arrastre del éter se produce en el dominio de un campo gravitónico, este arrastre tiene un
valor que depende inversamente del cubo de la distancia, por lo cual decrece muy
rápidamente. Ver sección 4.5.
6.3. Sentido del campo magnético.
Alrededor de una carga eléctrica en movimiento y en planos perpendiculares a la
trayectoria de la misma, encontraremos que los ejes de rotación de los eterones
constituyen una serie de curvas cerradas cuyos radios se extienden hacia el infinito. Estos
ejes de rotación determinan la dirección del campo magnético, tal como se muestra en la
fig. 6.3.1, en la cual se representa un plano único para no complicar demasiado la imagen.
q
fig. 6.3.1
Las líneas de inducción que hasta ahora eran una pura abstracción inventada para ayudar
a interpretar los campos magnéticos, adquieren con el éter una realidad física.
La figura 6.3.2. muestra la representación convencional de un campo magnético generado
por una corriente.
I
fig. 6.3.2
H
La física clásica ha establecido por convenio un determinado sentido del campo
magnético con relación al movimiento de las cargas eléctricas. Este sentido queda
determinado por la conocida “regla del sacacorchos” que se representa en la figura 6.3.3.
I
H
fig. 6.3.3
El sentido de giro de los eterones en un campo magnético resulta el inverso de una
corriente circular que produce el mismos efecto, debido a que el movimiento de giro se
transmite por el contacto de cargas que tienen signo opuesto, tal como se demuestra en
la figura 6.3.4, en la cual se comprueba cómo una corriente de cargas positivas hace girar
a los eterones que tienen carga negativa.
H
fig. 6.3.4
I
6.4. Intensidad del campo magnético.
La electrodinámica clásica nos demuestra que el campo magnético creado por una carga
eléctrica en movimiento a una distancia r tiene una intensidad cuyo valor es:
vqsenθ
H=
en u.em.
(6.4.1)
r2
El resultado se expresa en unidades electromagnéticas del sistema c.g.s. El ángulo θ es
el representado en la figura 6.2.2.
Cuando el campo se origina por una corriente en un conductor de longitud despreciable
respecto a la distancia r la intensidad resulta:
lIsen θ
H=
donde lI=vq
r2
La superficie esférica correspondiente a una distancia r tiene un área A que nos permite
expresar H en función de esta superficie de modo que:
vq sen θ
4πvq senθ
H=
=
u.em.
(6.4.2)
A
r2
Puesto que la intensidad del campo magnético es proporcional a la magnitud de la carga
móvil y a la velocidad de la misma, se deduce que dicha intensidad es proporcional a la
carga eléctrica de los eterones y a la velocidad tangencial de los mismos. En realidad un
eterón que está girando equivale a una espira recorrida por una corriente, excepto en el
sentido del campo que es de signo contrario, tal como se ha explicado en la sección 6.3.
El establecimiento de un campo magnético no se produce instantáneamente en todo el
espacio abarcado, sino que requiere un tiempo que está determinado por la velocidad de
propagación de las ondas electromagnéticas, que estudiaremos en la sección 7.2.
6.5. Comentario sobre las unidades electromagnéticas.
Cuando en el siglo XIX se descubrieron las primeras leyes del magnetismo, se estableció
la ley que rige la intensidad del campo creado por una carga móvil, con la ecuación 6.5.1
que dice:
vqsenθ
H=
u.e.m.
(6.5.1)
r2
Se aplicaron unidades del sistema c.g.s. como en electrostática, pero la unidad de medida
para la carga eléctrica resultaba 3x1010 veces mayor que el culombio de las unidades
electroestáticas (u.e.s.).
Cuando Maxwell en 1873 determinó la velocidad de propagación de las ondas
electromagnéticas a partir de medidas eléctricas y magnéticas, comprobó que la velocidad
resultaba la misma que se había medido experimentalmente para la velocidad de la luz:
C=3x1010 cm/s
aproximadamente
Esta velocidad de propagación de las ondas coincide con la relación que guardan entre sí
las unidades de carga eléctrica en los sistemas de u.e.m. y u.e.s. Esto permite expresar la
ecuación 6.4.1 en u.e.s. para tener:
vqsenθ
H=
u.e.s.
(6.5.2)
r2 c
Sabiendo que c es una velocidad de propagación nos preguntamos: ¿deberemos
considerar el factor c como un mero factor de proporcionalidad, o bien deberemos
considerar que realmente está implicada la velocidad de propagación en esta ley?
El autor se inclina por la segunda interpretación y opina que esta ley, como todas las del
electromagnetismo deberían sustituir el factor c por la velocidad de propagación u, de
modo que:
vqsenθ
H=
u.e.s.
(6.5.3)
r2u
En la cual u es la velocidad de propagación de las ondas electromagnéticas, y que
además no es constante, sino que depende de la densidad del éter, como se demostrará
más adelante en la sección 7.2.
En la electrodinámica clásica se ha establecido el concepto de flujo magnético Ф para
evaluar la magnitud total del campo magnético que aparentemente fluye a través de una
superficie normal a la dirección de las líneas de fuerza, de modo que:
Ф=Hn A
Ф=HAcosθ
Este concepto es imaginario, pues en la realidad no hay nada que fluya en la dirección de
las líneas de inducción de un campo magnético.
Aunque la denominación de “flujo” es poco realista, su utilización ha resultado muy
provechosa para resolver problemas en solenoides, transformadores, etc.
Considerando la existencia del éter, el “flujo magnético” adquiere un significado concreto
que podemos definir como la cantidad total de movimiento de carga eléctrica de los
eterones abarcados por una superficie normal a las líneas de inducción.
Ф=4 π∑ ve qe=HAn
Cuando las líneas de inducción tengan una inclinación respecto a la línea perpendicular a
la superficie, formando con la misma un ángulo θ, el flujo será:
Ф=HA cosθ
A
fig. 6.6.1
6.7. Influencia de los materiales en un campo magnético.
Los distintos materiales alteran la intensidad del campo debido a que los electrones son
cargas en movimiento de rotación y por lo mismo actúan de modo similar a los eterones.
La física clásica explica la influencia de los materiales sobre el flujo magnético de modo
compatible con la teoría del éter, por lo cual resultaría superfluo repetir aquí los mismos
razonamientos.
Al tratar los materiales magnéticos se introduce el factor de permeabilidad μ y a la
intensidad de campo resultante se la denomina inducción magnética B de modo que:
B=μH
En el sistema de unidades S.I. para el vacío se asigna un valor:
μo=4π 10-7
En el sistema de unidades c.g.s. para el vacío el valor es la unidad:
μ = 1
luego
B=H
Resulta evidente la ventaja que supone utilizar el sistema c.g.s. para obtener la máxima
sencillez en las ecuaciones.
6.8. Energía de un campo magnético.
La experiencia demuestra que en un campo magnético se almacena una cantidad de
energía cuya magnitud según la electrodinámica clásica es:
H2V
U=
u.e.m.
(6.8.1)
8π
Donde V es el volumen del campo considerado.
Si expresamos esta ecuación en unidades electrostáticas tendremos:
H2V
U=
u.e.s.
(6.8.2)
8πc2
y finalmente, de acuerdo con los criterios de la teoría del éter:
H2V
U=
u.e.s.
(6.8.3)
8πu2
La electrodinámica clásica no explica cómo puede almacenarse energía en un espacio
vacío, pero bajo los conceptos de la teoría del éter resulta evidente que la energía de un
campo magnético es simplemente la energía cinética de los eterones que están girando
dentro del campo.
En la sección 5.7 ya habíamos demostrado que la energía de un campo eléctrico tenía su
causa en el desplazamiento elástico de la carga de los eterones que acumulaban una
energía potencial cuyo valor es:
E2V
U=
u.e.s.
8π
Tanto la energía del campo magnético como la energía del campo eléctrico tienen su
equivalente en los sistemas mecánicos, pues mientras la primera equivale a la energía de
un volante de inercia, la segunda equivale a la energía de un muelle elástico que ha sido
tensado.
Por esta razón un circuito oscilante eléctrico se comporta del mismo modo que un volante
de reloj asociado a un muelle elástico.
En el fundamento de las leyes de la mecánica y de la electrodinámica subyace un origen
común, que habremos de descubrir paso a paso.
6.9. Magnitud y sentido de la fuerza magnética.
Cuando una carga eléctrica se desplaza en el seno de un campo magnético se produce
una fuerza que tiene siempre un sentido transversal respecto a la trayectoria de la carga y
también respecto a la dirección del campo magnético.
Se ha demostrado experimentalmente que la magnitud de esta fuerza es:
F=Hqvsenθ
u.e.m.
(6.9.1)
Hqv senθ
F=
u.e.s.
(6.9.2)
c2
Donde θ es el ángulo formado entre la trayectoria y la dirección del campo, según la fig.
6.9.1.
H θ
F
fig. 6.9.1
+q
Esta fuerza tiene un sentido que es independiente de la posición de la carga móvil que
origina el campo magnético. Se ha establecido por convenio el sentido del campo, y para
determinar el sentido de la fuerza se puede hacer uso de la denominada “regla de la
mano izquierda” que se representa en la figura 6.9.2.
fig. 6.9.2
Cuando la carga móvil se desplaza en la misma dirección del campo magnético no se
produce ninguna fuerza de acuerdo con la ecuación 6.9.2.
En el capítulo 8 se demostrará que las ecuaciones anteriores son solo correctas cuando
las cargas se desplazan a velocidades muy bajas respecto a la velocidad de propagación.
A velocidades altas es necesario aplicar un factor de eficacia que será determinado en
dicho capítulo.
Ya conocemos la ley que rige las fuerzas magnéticas y nos podemos preguntar: ¿cómo se
puede producir esta fuerza a distancia y por qué la fuerza resulta transversal a la
trayectoria?
6.10. El origen de la fuerza magnética.
Una vez explicado lo que es un campo magnético estamos en condiciones de
enfrentarnos con la explicación de las causas que producen las fuerzas magnéticas, que
tienen unas características muy peculiares y que hasta ahora han sido un enigma.
Ya hemos demostrado que la fuerza gravitatoria y la fuerza eléctrica a distancia tienen su
causa en la fuerza coeléctrica que se produce en el contacto de las partículas de materia
y el éter que está sometido a algún modo de alteración, rechazando el efecto directo de
las fuerzas a distancia. Seguidamente intentaremos explicar la fuerza magnética bajo los
mismos principios.
Para comprender el fenómeno analizaremos lo que sucede en los eterones que están en
contacto con las cargas eléctricas en movimiento, con la ayuda de la figura 6.10.1.
+q1
+q2
fig. 6.10.1
Para simplificar la imagen se representan unos poco eterones negativos, por ser éstos los
que tomarán contacto con las cargas móviles q1 y q2 que arbitrariamente hemos elegido
con signo positivo. También se ha elegido el movimiento de las cargas en el plano del
papel, de modo que la dirección del campo resulta normal al papel.
La rotación de los eterones está provocada por el efecto que producen ambas cargas y
por lo tanto la intensidad del campo magnético en cada punto del espacio será el
resultado de sumar las intensidades procedentes de q1 y q2 teniendo en cuenta su sentido.
En la figura se representa la intensidad de campo o su equivalente a la velocidad de
rotación de los eterones, por una flecha de longitud proporcional a esta velocidad.
La velocidad de rotación resulta diferente a cada lado de la trayectoria de las cargas
móviles, como consecuencia de sumar el propio efecto con el procedente de la otra carga.
Puede haber puntos en los cuales el campo magnético quede cancelado totalmente.
En esta representación se ha dado un tamaño exagerado a los eterones, para no
complicar la figura, pero deberemos entender que los eterones serán muy pequeños
respecto a las partículas con carga y, por consiguiente, éstas tomarán contacto con
numerosos eterones al mismo tiempo.
En la fig. 6.10.1 aparecen las fuerzas magnéticas F1 y F2 perpendiculares a las trayectorias
de las cargas respectivas.
Para explicar el origen de estas fuerzas nos serviremos
de la fig. 6.10.2 en la cual aparecen las fuerzas
coeléctricas Fa y Fb actuando sobre la carga móvil +q2 de
la figura anterior. Podemos observar que existe una
diferencia en la velocidad de rotación de los eterones a y
b que tienen contacto con la carga q2. De aquí deducimos
+q2
que para que resulte una fuerza F2 es necesario que las
fuerzas coeléctricas Fa y Fb sean de diferente magnitud,
de modo que F2 = Fa-Fb.
También se deduce que las fuerzas coeléctricas son
dependientes de la velocidad de rotación, de modo que
disminuyen al aumentar la velocidad. En el capítulo 8 se
fig. 6.10.2
demostrará la dependencia que existe.
EL CAMPO ELECTROMAGNÉTICO
7.1. Inducción electromagnética.
El fenómeno de la inducción de un campo eléctrico por la variación de un campo
magnético tiene una explicación razonada basada en las propiedades del éter dieléctrico,
del mismo modo que puede explicar las ondas electromagnéticas.
Desde que Michael Farady y Joseph Henry, separadamente, descubrieron las leyes de
este fenómeno, se hicieron grandes avances que culminaron con las ecuaciones de
Maxwel.
A partir de ese momento, la errónea creencia de la propagación de las ondas en el vacío,
concebida por el propio Maxwell y después corroborada por Einstein en su teoría de la
relatividad Especial, ha bloqueado la posibilidad de seguir avanzando en un conocimiento
más profundo de las leyes físicas, mientras la tecnología ha progresado de un modo
vertiginoso.
Basándose en las leyes que rigen los fenómenos electromagnéticos, Maxwell dedujo las
leyes de la propagación de las ondas electromagnéticas y pudo determinar su velocidad,
la cual resultó ser la misma que tiene la luz.
Con la teoría del éter procederemos en sentido inverso, pues partiendo del conocimiento
de la propagación del movimiento rotacional en un medio elástico, de acuerdo con los
principios de la mecánica clásica, podremos explicar cómo se producen los fenómenos
electromagnéticos, cuyas leyes conocemos pero cuyas causas ignoramos.
Demostraremos que las leyes de la electrodinámica son una consecuencia de la
propagación en el éter y no su causa, como se ha considerado hasta ahora.
A lo largo de este trabajo veremos como desaparece la separación que actualmente se
mantiene entre los fenómenos mecánicos y los fenómenos eléctricos, comprobando que
unos y otros están tan íntimamente relacionados que no podrían tener una existencia
independiente.
7.2. Propagación rotacional en el éter.
En la física clásica se ha estudiado la propagación del movimiento transversal en un
medio elástico y también la propagación de un movimiento longitudinal, pero nunca se ha
tratado la propagación de un movimiento rotacional, lo cual vamos a hacer seguidamente.
Cuando la intensidad de un campo magnético sufre una
variación, cambia la velocidad de rotación de los eterones
ΔV
u
y este cambio se propaga en el éter a una velocidad
determinada (u) según ilustra la fig. 7.2.1.
En la periferia de los eterones la alteración se propagará a
una velocidad (vp) determinada por la densidad de masa y fig. 7.2.1
el módulo de elasticidad B de los mismos.
ΔV
u
En el éter resultará una velocidad para el frente de onda
que tendrá un valor medio:
2vp
u=
π
de acuerdo con la fig. 7.2.2.
fig. 7.2.2
La mecánica clásica demuestra que la velocidad de
propagación de una onda longitudinal es:
B
u=√
ρ
Donde B es el módulo de elasticidad y ρ es la densidad del medio.
Es conveniente reproducir la demostración de esta ley porque nos servirá posteriormente
para explicar el fenómeno de la inducción de un campo eléctrico a causa de la variación
de un campo magnético.
En la fig. 7.2.3 se representa un tubo lleno de un fluido que tiene una densidad ρ con una
presión en reposo de valor P.
El tubo tiene una sección transversal con una superficie A y está provisto de un émbolo
que puede deslizarse a lo largo del mismo.
En el instante to se pone en movimiento el émbolo con una velocidad v. Después de un
tiempo t todo el fluido contenido entre los límites a y b se habrá puesto en movimiento con
velocidad v, mientras el resto permanece todavía en reposo. El límite b avanza hacia la
derecha con la velocidad de propagación vp.
F
A
V+p
Vp
F
V
A
Vt
fig. 7.2.3
a
b
Cuando el pistón ha recorrido la distancia vt el volumen ha disminuido en una cantidad
que resulta -∆V=vtA.
ΔPV
Sabiendo que el módulo de compresibilidad es B=
ΔV
-ΔVB
resulta
ΔP=
y como -ΔV =vtA
y V =vp tA
V
vtAB
vB
tendremos
ΔP=
luego ΔP=
(7.2.1)
vp tA
vp
La fuerza ejercida sobre el pistón vale F=∆PA que actuando durante un tiempo t
producirán un impulso p=Ft=∆PAt donde al sustituir ∆P por su valor
nos lleva a:
BAtv
p=
vp
La cantidad de masa puesta en movimiento es la que ocupaba inicialmente el volumen
vptA con una densidad ρ por lo que m=ρvptA y la cantidad de movimiento resultará:
mv=ρvptAv
Como el impulso recibido debe igualar a la cantidad de movimiento tendremos:
BAtv
B
=ρvptAv
de donde
B = ρv2
(7.2.2)
vp
y por consiguiente vp=√ρ
Debido a que no conocemos con exactitud como está distribuida la carga eléctrica de los
eterones que toman contacto con seis eterones de signo opuesto, además de que los
eterones esféricos no ocupan la totalidad del espacio vacío, podemos estimar que la
ecuación 7.2.2 aplicada al éter como conjunto dará un resultado ligeramente superior al
valor real.
No obstante podemos asumir que a pesar de esa desviación el resultado habrá de ser
proporcional al expresado por la ecuación 7.2.2 por lo cual podemos establecer otra
ecuación donde el módulo de compresibilidad B quede modificado por un factor adecuado
de modo que KB=Y.
La nueva ecuación será entonces:
Y
(7.2.3)
u=√
ρ
Donde u = velocidad de las ondas electromagnéticas
Y = módulo de compresibilidad condicionado
ρ = densidad del éter
Esta ecuación no nos permite calcular el valor numérico de la velocidad de propagación
debido a que no conocemos todavía la densidad del éter ni el módulo Y pero nos da a
conocer la relación cualitativa que existe entre las tres magnitudes, lo cual nos será de
gran utilidad.
Hasta ahora, siempre que se había intentado encontrar un medio de propagación para las
ondas electromagnéticas o para la luz, se buscaba un medio capaz de propagar ondas
transversales, pero ningún material conocido tenía las propiedades adecuadas para
propagar tales ondas a una velocidad tan elevada.
En la propagación rotacional no se propagan ondas transversales, sino longitudinales,
sobre los eterones. Pero debido a la rotación de los eterones surgen campos eléctricos y
magnéticos que tienen un sentido transversal respecto a la dirección de propagación
cuando se produce alguna aceleración en la velocidad de giro, tal como será demostrado
en la sección siguiente.
La ecuación 7.2.3. solo es válida para la propagación de los campos electromagnéticos,
en los cuales se produce la rotación de los eterones, pero en los campos gravitatorios en
los cuales no interviene el movimiento rotacional, la onda gravitatoria se propagará
directamente a través de los eterones y por consiguiente la velocidad que resulte quedará
π
aumentada por el factor
2
7.3. El desplazamiento transversal.
Para poder explicar como se induce un campo eléctrico por la variación de un campo
magnético, deberemos analizar previamente el comportamiento de los eterones al
propagar en movimiento de rotación, porque ello nos llevará a la demostración de que el
campo eléctrico es la consecuencia del desplazamiento de la carga eléctrica de los
eterones cuando su movimiento de rotación es sometido a una aceleración.
Para estudiar este fenómeno nos serviremos de un modelo similar al que ya hemos
utilizado para explicar la velocidad de propagación de una onda, porque ambos
fenómenos están estrechamente relacionados.
Analizaremos lo que sucede en un circuito toroidal lleno de un fluido elástico, aplicando
los mismos criterios utilizados para deducir la velocidad de propagación.
Consideremos un tubo de forma toroidal, provisto de un
p
V
pistón, que tiene una sección de área A, según se muestra
en la fig. 7.3.1.
V
Si movemos el pistón con una velocidad constante v a lo
a
largo del tubo anular, delante del mismo se producirá un
b
incremento de presión ∆P y su frente avanzará con la
correspondiente velocidad de propagación vp. Al mismo
tiempo, detrás del pistón se producirá una disminución de
presión -∆P, cuyo frente avanzará en sentido opuesto con
fig. 7.3.1
-Vp
velocidad -vp.
Transcurrido un tiempo t después de iniciarse el movimiento, sucederá que el frente de
presión delantero habrá dado una vuelta completa alcanzando al pistón por detrás,
mientras el frente posterior, avanzando en sentido contrario, habrá alcanzado al pistón por
su parte delantera, resultando de esto que el incremento de presión en la parte delantera
quedará neutralizado por el decremento de presión procedente de la parte trasera y
viceversa, por lo cual todo el anillo quedará con la presión inicial.
En el caso de que la velocidad del pistón resulte despreciable respecto a la velocidad de
propagación, el tiempo necesario para que el frente de presión recorra el circuito completo
será:
2 πr
ℓ
t=
=
vp
vp
A partir de este momento todo el fluido del anillo tendrá la misma presión y avanzará con
la misma velocidad que el pistón, comportándose como un volante de inercia.
Supongamos ahora que en el mismo dispositivo le aplicamos al pistón un movimiento
uniformemente acelerado.
Recordemos que delante del pistón y antes de ser alcanzado por el frente de presión
procedente de la parte posterior, se producirá un incremento de presión, de acuerdo con
la ecuación 7.2.1:
Bv
ΔPa =
vp
En el mismo instante detrás del pistón tendremos un decremento de presión que será:
-Bv
ΔPb =
vp
Para que un frente de presión recorra todo el anillo necesita un tiempo que es
ℓ
t=
vp
por lo tanto cuando el frente de presión posterior alcance el pistón en su parte delantera,
este ya habrá aumentado su velocidad en:
aℓ
Δv=at=
vp
Al incremento de presión delante del pistón se le sumará el incremento negativo
procedente de la parte posterior y tendremos:
B(v+Δv)
Bv
BΔv
Ba ℓ
ΔPa=
-
=
=
2
vp
vp
vp
v
p
Del mismo modo, detrás del pistón resulta:
-Baℓ
ΔPb=
2
v
p
La presión en el toroide será decreciente desde la cara a del pistón donde alcanza su
valor máximo, hasta la cara b donde se produce su valor mínimo, pasando por su valor
medio en la región diametralmente opuesta al pistón.
En la fig. 7.3.2 se representa la distribución de la presión decreciente desde a hasta b.
a
a
A
A
b
fig. 7.3.2
Baℓ
-Baℓ
ΔP
=
mientras
ΔPb=
a
2
v2
v
p
En la mitad superior del toroide tendremos un incremento medio de presión:
-Baℓ
mientras en la mitad inferior: ΔP=
2
2v
p
Este resultado significa que la aceleración ha producido un desplazamiento de masa
hacia la mitad superior, cuya magnitud ∆m podemos calcular para el caso de un toroide de
masa m con una longitud ℓ, utilizando las relaciones que ya conocemos:
Ba ℓ
-ΔPV
m=ρV ΔP=
ΔV =
B
2v2
La cantidad de masa desplazada será Δm= ΔρV
m
m
-mΔV
-mΔV
donde Δρ=
-
=
luego Δm=
V +ΔV
v
V2+VΔV
V +ΔV
-ΔPV
ρVΔP
donde ΔV =
y
m = ρV
luego Δm=
B
B-ΔP
Ba ℓ
donde ΔP=
y ρV = m
luego
= masa desplazada md
2
2v
p
En el caso de aplicar esta ecuación al caso de los eterones, encontraremos que el término
(aℓ ) resulta despreciable frente a 2 v2
por lo que podemos eliminarlo en el denominador y
tendremos:
am ℓ
md =
(7.3.1)
2
2v
p
7.4. El campo eléctrico radiado.
El fenómeno del desplazamiento de la masa en un movimiento de rotación acelerada nos
va a permitir demostrar que este desplazamiento es la causa para que se produzca un
campo eléctrico transversal al propagarse en el éter una variación del campo magnético.
Cuando una carga eléctrica sufre un movimiento con aceleración, este se transmite a los
eterones contiguos y se propaga en el éter con la velocidad propia de este medio (u) de
acuerdo con la fig. 7.4.1 en la cual solo se ha representado una fila de eterones.
a
q
fig. 7.4.1
Conocemos ya el desplazamiento de masa que se produce en un anillo toroidal cuando es
sometido a una aceleración, pero los eterones deberán ser esféricos y su distribución de
masa queda afectada por el contacto con otros seis eterones de signo opuesto. Por otro
lado la impulsión se aplica en un punto de la superficie en vez de aplicarla con un pistón
como en el toroide. Todo lo anterior hace extremadamente difícil evaluar con precisión
cual será el desplazamiento de masa en los eterones, pero podemos asumir que será
proporcional al que se produce en un anillo.
La masa desplazada en un anillo del acuerdo con la ecuación 7.3.1 es:
amℓ
amπR
md =
donde ℓ=2 πR
luego
md=
2
2v2
v
p
πu
La velocidad en la periferia es vp =
2
siendo u la velocidad de propagación en el éter, por lo cual tendremos:
4 amR
md=
πu2
En un eterón esférico la masa desplazada resultará proporcional a la anterior con un
factor kd que no podemos determinar actualmente, pero nos permite establecer que:
amR
kd
md =
u2
El conocer el valor exacto de kd no sería de mucha utilidad, puesto que todavía no
conocemos el valor de la masa y el radio del eterón.
Finalmente, asumiendo que la carga eléctrica de los eterones es proporcional a su masa,
podemos establecer que la carga desplazada será:
kdaQR
qd=
(7.4.1)
u2
Donde Q es la carga del eterón y R es el radio del mismo.
En una región del éter donde no haya campo eléctrico y exista un campo magnético
estacionario, las cargas eléctricas abarcadas por una superficie determinada estarán
equilibradas, tal como se muestra en la fig. 7.4.2.
E=0
V
fig. 7.4.2
E=0
E
u
a
fig. 7.4.3
E
Sin embargo cuando se propaga una aceleración rotacional, la carga eléctrica de los
eterones positivos se desplaza en un sentido mientras la carga de los eterones negativos
se desplaza en el sentido contrario, según se muestra en la fig. 7.4.3, dando lugar a que
sobre la superficie considerada se acumule una carga neta que originará un campo
eléctrico cuya intensidad, de acuerdo con la ecuación 5.1.3 será:
4 πqd
E=
(7.4.2)
A
Donde qd es la carga desplazada sobre la superficie A.
La carga desplazada en un eterón según la ecuación 7.4.1 es:
KdaQR
qd=
u2
mientras que la superficie ocupada es A= 4R2, por lo cual resulta:
πKdaQ
E=
(7.4.3)
Ru2
Este resultado demuestra que el campo eléctrico radiado se produce por el
desplazamiento transversal de la carga de los eterones cuando se aceleran.
7.5. El campo magnético radiado.
El desplazamiento transversal de la carga eléctrica, provocado por la aceleración de los
eterones, avanza en el éter a la velocidad de propagación u, lo cual equivale a una carga
qd moviéndose a esta velocidad, como ilustra la fig. 7.5.1. Ya vimos en la sección 6.4. que
la intensidad de campo magnético estaba determinada por la cantidad de movimiento de
carga eléctrica por superficie unitaria, de acuerdo con la ecuación 6.4.3.
u
+qd
a
fig. 7.5.1
u
-q
d
4π vq
4πuqd
H=
luego
Hr=
(7.5.1)
A
A
4 πqd
Como el campo eléctrico radiado es:
Er =
A
Encontramos que Hr=Eru en u.e.s. ambos.
(7.5.2)
Estos campos se desplazan, ambos asociados, a la velocidad de propagación propia del
éter y son campos radiados que deberemos distinguir de los campos estacionarios, por lo
cual los designaremos en adelante con los símbolos Er y Hr para evitar confusiones.
En el campo magnético radiado (Hr) su magnitud depende de la aceleración en la rotación
de los eterones, mientras en el campo magnético estacionario (H) su magnitud es función
de la velocidad de rotación. Esto explica cómo es posible que el campo radiado alcance
un valor máximo cuando el campo magnético puede pasar por un valor nulo.
Podemos expresar el valor de Hr en función de la aceleración rotacional de los eterones a
partir de las ecuaciones que ya conocemos:
πKdaQ
πKd aQ
Hr=Er u
y
Er=
luego
Hr=
Ru2
Ru
La dirección del campo magnético será perpendicular a la dirección de la propagación y
también perpendicular al campo eléctrico.
7.6. Campo electromagnético radiado por una carga acelerada.
Hasta aquí hemos explicado el campo electromagnético en relación con la aceleración de
los eterones, sin considerar la causa que lo origina, que puede ser una carga con
movimiento acelerado o su equivalente de una corriente variable que circula dentro de un
conductor.
La electrodinámica clásica demuestra que una carga eléctrica acelerada radia un campo
eléctrico y otro magnético perpendiculares entre sí y respecto a la dirección de
propagación, tal como se representa en la fig. 7.6.1.
a
θ
q
Fig. 7.6.1
Las intensidades de estos campo a una distancia r desde la carga móvil son las
siguientes:
aqsenθ
Er =
en u.e.s.
(7.6.1)
rc2
aqsenθ
Hr =
en u.e.s.
(7.6.2)
rc
Podemos hacer una comparación entre las ecuaciones establecidas por la
electrodinámica clásica para los campos electromagnéticos originados por una carga
acelerada y las ecuaciones propuestas en esta teoría del éter en función de la rotación
acelerada de los eterones. Para ello tomaremos las mismas condiciones y usaremos las
mismas unidades de medida que serán u.e.s. en c.g.s.
Carga acelerada: con sen θ=1
Eterón acelerado: con u=c
πkdaQ
aq
Er=
Er=
rc2
Rc2
πkdaQ
aq
Hr=
Hr=
rc
Rc
Resulta evidente la congruencia entre los dos grupos de ecuaciones, lo que corrobora que
el éter es el soporte de los campos electromagnéticos.
En ambos casos hemos utilizado la velocidad de propagación c para respetar la expresión
clásica, pero de acuerdo con la teoría del éter debería utilizarse el símbolo u que no es
una constante.
7.7. Ondas electromagnéticas senoidales.
Cuando la radiación electromagnética es provocada por una corriente alterna que varía
senoidalmente, los campos radiados Er y Hr están adelantados en fase un ángulo π /2
respecto a la corriente del elemento emisor y también respecto del campo magnético
estacionario, tal como demostraremos a continuación.
Sabemos que los campos radiados Er y Hr son función de la aceleración de la carga
eléctrica:
∂vq
∂H
Hr =Er u=(f )a=(f )
=( f )
∂t
∂t
Cuando la corriente del sistema emisor varía senoidalmente su valor instantáneo es:
i=Isenwt
donde I es el valor máximo de la corriente y
w=2πf
También sabemos que el campo magnético estacionario H es función de la corriente:
H=(f)i luego
H=(f)Isenwt
Mientras que los campos eléctricos y magnéticos radiados dependen de la variación del
campo magnético estacionario, de modo que:
∂i
∂i
Hr=Er u=(f)
donde
=Icoswt
∂t
∂t
Por consiguiente los campos radiados resultarán:
Hc=Eru=(f)Icoswt
Este resultado significa que los campos radiados Er y Hr están adelantados en fase a un
ángulo
respecto a la corriente del emisor y también respecto del campo magnético
estacionario H, los cuales están ambos en la misma fase.
Considerando la posición en el espacio, este adelanto de fase equivale a un adelanto de
¼ de longitud de onda.
En la fig. 7.7.1 se representan gráficamente las intensidades de los campos eléctricos y
magnéticos radiados por un dipolo que se alimenta con una corriente senoidal.
λ
Er
i
Er
Hr
i
Hr
Hr
fig. 7.7.1
Er
Para evitar una figura demasiado confusa no se ha representado el campo magnético
estacionario que debe estar retrasado ¼ de longitud de onda respecto a los campos
radiados Er y Hr. La longitud de onda depende de la frecuencia y de la velocidad de
propagación:
u
λ=
f
El hecho de que en la electrodinámica clásica se confundan el campo magnético radiado
y el campo magnético estacionario, da lugar a que se intente explicar por qué los campos
radiados Er y Hr están en la misma fase a cierta distancia del emisor y sin embargo no lo
están en las proximidades del mismo.
La realidad es que el campo radiado Hr y el campo estacionario H son dos cosas distintas
y siempre están desfasados entre sí, mientras los campos Er y Hr siempre están en fase
entre sí.
Cuando algún autor consigue explicar las causas de ese imaginario cambio de fase
mediante oscuros y largos razonamientos, deberemos pensar que comete algún error,
pues realmente no es posible explicar el citado cambio de fase por la sencilla razón de
que no existe ningún cambio.
7.8. Flujo de energía radiada.
La energía del campo eléctrico contenido en un volumen V de éter es:
E2V
UE=
en u.e.s.
8π
Mientras que la energía del campo magnético en el mismo volumen es:
H2V
UH=
en u.e.s.
8πu2
La relación entre los campos radiados es: Hr=Eru
E
2u2V
E2V
r
Por lo tanto UH =
=
=UE
luego
UH=UE
8π
8πu2
Lo cual demuestra que la energía de los campos radiados, es la misma en el campo
eléctrico que en el campo magnético asociado, de modo que la energía total es:
2E
2V
E2V
r
UT =UE+UH=
=
(7.8.1)
8π
4π
Esta energía se desplaza en el éter a la velocidad de propagación y por lo tanto constituye
un flujo de energía cuya potencia podemos determinar.
Consideramos un espacio cúbico según la fig. 7.8.1 en la
l
cual el volumen será:
V=Aℓ
E2 Aℓ
r
por lo tanto
UT=
u
4π
l
En un tiempo t=
toda la energía contenida en el
u
volumen habrá pasado a través de la superficie A.
fig. 7.8.1
E2utA
r
Sustituyendo
por su equivalente ut tendremos:
UT=
4π
E
2uA
U
r
La potencia está definida por:
P=
por lo cual resulta:
P=
(7.8.2)
t
4π
Esta ecuación nos expresa la magnitud de la potencia que incide sobre una superficie en
función de la intensidad del campo eléctrico recibido de una radiación electromagnética.
Se puede determinar la potencia incidente sobre una superficie en relación con la carga
eléctrica acelerada que ha originado la radiación electromagnética.
De acuerdo con la ecuación 7.6.1 la intensidad del campo eléctrico radiado, a una
distancia r tiene una magnitud que es:
aqsenθ
Er=
ru2
Sustituyendo este valor en la ecuación 7.8.2 obtenemos:
2
aqsenθ
Au
a2 q2 sen2θA
luego
P=
P=(
)
4π
ru2
r2 4πu3
Este resultado nos demuestra que la potencia que incide sobre una superficie es
inversamente proporcional al cuadrado de la distancia y además depende del ángulo θ de
a cuerdo con la fig. 7.8.2.
Integrando la potencia que pasa a través de la superficie
esférica completa con radio r, obtendríamos la potencia
total radiada por la carga eléctrica acelerada y el resultado
θ
sería:
a
2 aq
P=
(7.8.4)
r
3u3
q
fig. 7.8.2
Anteriormente habíamos hecho constar que las leyes de la electrodinámica son la
consecuencia de la propagación de un campo electromagnético en el éter y no su causa,
como se ha interpretado hasta ahora.
Esta es la razón para que podamos explicar la conocida ley de Faraday basándonos en el
conocimiento de la naturaleza de los campos electromagnéticos que se propagan en el
éter.
La ley de Faraday nos dice que cuando varía el flujo magnético abarcado por un circuito
cerrado se genera un potencial eléctrico cuyo valor es igual a la derivada de la variación
del flujo respecto al tiempo. Esta ley se estableció usando las unidades de medida
conocidas como unidades electromagnéticas (u.e.m.) y su expresión matemática es:
∂φ
V =-
u.e.m.
∂t
H
Ф = HA1
fig. 7.9.1
Considerando el campo eléctrico distribuido a lo largo del circuito la ley se expresa del
modo siguiente: Ф
∮E∂ℓ=-∂Ф
u.e.m.
∂t
Seguidamente demostraremos que este fenómeno tiene su causa en la radiación de un
campo electromagnético que se produce cuando el flujo estacionario sufre una variación.
Para ello nos ayudará la fig. 7.9.2.
A2
∞
A1
fig. 7.9.2
El flujo neto abarcado por la superficie A1 debe ser igual al flujo neto extendido en el plano
infinito A2 pero con sentido contrario.
Por lo tanto, a una variación del flujo neto abarcado por A1 corresponderá una variación
igual del flujo contenido en A2:
ΔФ1 = ΔФ2
Pero mientras ΔФ1 es un incremento del flujo estacionario contenido en la superficie A1, el
ΔФ2 es una variación de flujo que se extenderá sobre la superficie A2 a la velocidad de
propagación correspondiente, constituyendo un flujo radiado que designaremos como Фr y
que tendrá sentido contrario a Ф1. Por lo tanto,
ΔФ=-Фr
Consideremos el caso de una espira circular según la fig. 7.9.3 que encierra un superficie
A1 y que el flujo contenido en la misma sufre una variación durante un tiempo dt
provocando una diferencia de flujo dФ. De modo que
d Ф=-Фr
A1
dr
fig. 7.9.3
A2
El flujo Фr radiado durante un tiempo dt ocupará una corona circular con una anchura
dr=dtu; y esta corona avanzará sobre el plano infinito A2 con velocidad u.
La superficie de esta corona será:
Ac=2π rdr
A1
dr
fig. 7.9.4
A2
Según se representa en la fig. 7.9.4 y por consiguiente la intensidad del campo magnético
radiado será:
Фr
-dФ
-dФ
Hr =
=
de donde
2πrHr =
Ac
2πrdr
dr
donde dr=dtu
-dФ
-dФ
luego
2πrHr =
y por lo tanto
2πrHru=
u.e.s.
(7.9.1)
dtu
dt
La ley de Faraday fue establecida usando el sistema de unidades electromagnéticas,
mientras que en esta teoría del éter utilizamos el sistema de unidades electrostáticas que
habremos de considerar (ver sección 6.5.).
Sabemos que la relación entre la intensidad del campo magnético radiado y la intensidad
del campo eléctrico asociado según 7.5.2 es: Hr=Eru en u.e.s. que expresado en u.e.m.
resulta Hru=Er
Por consiguiente, la ecuación 7.9.1 expresada en u.e.m. resultará
-dФ
2πrEr=
dt
Si tenemos una espira circular con radio r según la fig. 7.9.5 podemos sustituir 2πr por su
equivalente
que es la longitud de la espira y obtendremos:
-Ф
ℓEr=
donde
ℓE=V
dt
-dФ
luego
V=
(7.9.2)
dt
Ф
fig. 7.9.5
Con este resultado hemos llegado hasta la ley de Faraday, partiendo de la propagación de
los campos electromagnéticos. Se demuestra que en un circuito con cualquier forma, que
encierra un flujo magnético, cualquiera que sea la separación, se cumple que:
∮ Ed ℓ=-dФ
en u.e.m.
(7.9.3)
dt
Ф
fig. 7.9.6
Si se considera únicamente la variación del flujo magnético en el tiempo, resulta imposible
explicar cómo se genera un potencial eléctrico en las espiras que rodean el núcleo de un
transformador, puesto que están situadas en un espacio donde no hay flujo, ya que éste
queda confinado dentro del núcleo. Sin embargo el fenómeno queda perfectamente
justificado al considerar el campo electromagnético radiado que se propagará a través del
espacio donde se sitúan las espiras.
MODIFICACIÓN EN LA ELECTRODINÁMICA
8.1. Controversia sobre la masa y la carga eléctrica.
En las primeras décadas del siglo XX se realizaron varios experimentos para determinar
la relación existente entre la carga eléctrica y la masa de los electrones, basados en la
deflexión de la trayectoria de los electrones de alta velocidad cuando atraviesan campos
eléctricos y campos magnéticos.
En estos experimentos se trataba de confirmar el postulado de la teoría de la Relatividad
Especial, según el cual la masa de las partículas en movimiento debe aumentar de
acuerdo con la siguiente ley:
1
m=mo
v2
√1-
c2
donde m es la masa en movimiento, m0 es la masa en reposo, v es la velocidad de la
partícula y c es la velocidad constante de la luz.
En el año 1939 M.M. Rogers, A. W. Mc. Reynolds y F.T. Rogers determinaron de forma
muy precisa la relación masa-carga utilizando los electrones correspondientes a tres
líneas netas del espectro de rayos β emitidos por el radio.
En una primera fase se determinaba la cantidad de movimiento de los electrones
mediante un dispositivo como el representado en la fig. 8.1.1 en el cual los electrones
atraviesan un campo magnético que se ajusta para conseguir la mayor incidencia sobre el
contador. Los electrones inciden sobre el contador cuando la fuerza magnética iguala a la
fuerza centrífuga, de modo que:
2
mv
m
Hr
Hvq=
luego
mv=Hqr
resultando
=
r
q
v
Después se realizaba la deflexión de los electrones mediante el dispositivo de la fig. 8.1.2
que dispone de dos placas curvadas P1 y P2 entre las cuales se aplica una diferencia de
potencial ajustable para lograr la máxima incidencia sobre el contador.
Ahora se deberá cumplir que la fuerza centrífuga iguale a la fuerza eléctrica, de modo
que:
2
mv
Eq=
R
Campo H normal
V
E=
al plano del
dR
papel
r
R
+
Emisor rayos β
Emisor rayos β
fig. 8.1.1
fig. 8.1.2
Conociendo los valores de los campos eléctrico y magnético se puede determinar la
velocidad y la relación masa-carga:
mv = Hqr
mv
Emv
mv2
E
v
ER
m
Hr
m
2
} q=
;
=
;
=
;
v=
;
=
luego
=(Hr)2
mv
Eq =
Hr
Hr
R
Hr R
Hr
q
v
q
ER
R
El resultado de los experimentos demostró que esta última ecuación solo se cumplía si se
introducía un factor denominado factor gamma
2
1
mo
moγ
γ=
luego
=(Hr)
=(Hr)2
2
ER
q
ER
v
v
√1-c2
q√1-
c2
Donde mo es la magnitud de la masa en reposo y moγ el valor que la masa alcanza a la
velocidad v.
Este resultado reforzó la creencia de que la masa aumentaba con la velocidad y quedaba
multiplicada por el factor γ.
Pero también es razonable pensar que la masa permanece constante y que es la carga
eléctrica la que disminuye con la velocidad de modo que:
2
v
q=qo√1-c2
lo cual nos lleva al mismo resultado que expresaríamos así:
m
=(Hr)2
2
ER
v
qo √1-
c2
¿Cuál es la verdadera interpretación? ¿Crece la masa? ¿Disminuye la carga eléctrica al
aumentar la velocidad?
Ambas interpretaciones son igualmente legítimas, pero también igualmente difíciles de
aceptar si no se justifica este cambio de magnitud por alguna razón. ¿Cómo pueden
cambiar la masa o la carga eléctrica por el mero hecho de desplazarse en el vacío? ¿Hay
alguna otra razón que pueda justificar este comportamiento sin alterar la magnitud de la
masa o de la carga eléctrica? La contestación es afirmativa y tendrá su explicación en la
sección siguiente.
8.2. Solución al enigma de la masa y la carga eléctrica.
La presencia del éter nos va a permitir explicar el comportamiento de los electrones que
se ha descrito en la sección anterior, como la consecuencia de un cambio en el campo
eléctrico motivado por el movimiento de las cargas eléctricas en el seno del éter.
El campo eléctrico en torno a la carga móvil sufre una disminución debido a la rotación
impuesta a los eterones y como consecuencia de esto disminuye la fuerza ejercida sobre
la propia partícula. No cambia la eficacia de la carga para producir el campo magnético;
por lo tanto podemos afirmar que no cambia la magnitud de la carga eléctrica, solo
cambia el campo eléctrico.
Al explicar el origen de la fuerza magnética en la sección 6.9. habíamos encontrado que
esta fuerza tiene una dependencia de la rotación de los eterones, debido a que el campo
eléctrico es alterado por este movimiento de rotación.
Ante este fenómeno nos preguntamos: ¿es posible evaluar esta alteración del campo
eléctrico, provocada por el movimiento de la carga?
El hecho de que una carga eléctrica desplazándose a través del éter se comporte como si
hubiera disminuido su campo eléctrico, mientras aumenta el campo magnético, nos
induce a pensar que se está cumpliendo el principio de la conservación de la energía, que
en este caso es la energía potencial del campo eléctrico y la energía potencial del campo
magnético, ambos dimanantes de la misma carga eléctrica. Hagamos la prueba:
Sabemos que la energía almacenada en el éter por los campos eléctrico y magnético, en
un volumen determinado es respectivamente:
E2V
H2V
UE=
u.e.s.
UH=
u.e.s.
8π
8 πc2
Si consideramos que la energía potencial de una partícula con carga eléctrica debe
mantenerse constante cuando se desplace en el éter, deberá cumplirse que la energía en
reposo debida al campo eléctrico sea igual a la suma de la energía de los campos
eléctricos más la energía del campo magnético originado por el movimiento:
UEo=UEv +UH
Si intentásemos calcular la relación entre los campos de una partícula en movimiento con
los campos de una partícula en reposo, necesitaríamos recurrir a unos cálculos de
integración muy complicados, pero sin embargo podemos utilizar un caso particular que
nos proporciona una solución muy sencilla.
Este es el caso de un conductor de longitud infinita o muy grande respecto a la distancia
(r) considerada, en el cual resulta una distribución cilíndrica para la intensidad de ambos
campos.
En la fig. 8.2.1 se representa el campo magnético creado por una corriente en un
segmento de longitud d
sobre un conductor de longitud muy grande. La superficie
cilíndrica con radio r es el lugar geométrico de todos los puntos del espacio con la misma
intensidad de campo H.
dq
dl
H
dl
E
I
r
r
fig. 8.2.1
fig. 8.2.2
Aplicando las leyes de la electrodinámica al caso de la fig. 8.2.1 tendremos:
2I
dq
vdq
2vdq
H=
;
I=
=
;
H=
r
dt
dℓ
rd ℓ
La misma carga dq en reposo sobre la misma longitud d
, según la fig. 8.2.2 creará un
campo eléctrico cuya intensidad será:
2dq
E=
rd ℓ
Consideremos ahora que la suma de energía del campo eléctrico y del campo magnético
es una cantidad constante y aplicamos los valores correspondientes a un pequeño
volumen de éter situado a una distancia r, expresando la energía de ambos campos en el
mismo sistema de unidades u.e.s.
2
E
2V
E2V
H2V
H
o
v
UEo=UEv +UHv
;
=
+
;
E2=E2+
8π
8π
8 πc2
c2
2
2 vdq
2
2
2
H
E
H
v
v
v
( rd ℓ ) v2
E2=E2-
;
=1-
=1-
=1-
2
c2
E2
E2c2
c2
c2
(2dqrdℓ)
2
E
v
v2
v2
Teniendo
=1-
resulta que
E2
c2
Ev=Eo√1-c2
Este resultado nos permite afirmar que la eficacia de una carga eléctrica para generar un
campo eléctrico, depende de la velocidad de dicha carga respecto al éter, de modo que:
2
v
qef=qo √1-c2
Esta ecuación está de acuerdo con el resultado de los experimentos descritos en la
sección 8.1., puesto que:
m =m
=(Hr)2
qef
ER
v2
q√1-
c2
Por consiguiente queda demostrado que la masa no aumenta con la velocidad, como
postula la Relatividad Especial, sino que se produce una disminución del campo eléctrico
cuando una carga se desplaza en el éter provocando la rotación de los eterones.
Es conveniente insistir en el hecho de que la carga eléctrica mantiene una magnitud
constante cuando se desplaza a cualquier velocidad y que su eficacia para producir un
campo magnético es la misma que se ha considerado hasta ahora. Lo que realmente
sucede es que para mantener constante la energía potencial de la carga eléctrica, es
necesario que disminuya el campo eléctrico cuando aumenta el campo magnético, tal
como ha quedado demostrado.
Cuando una partícula con carga eléctrica se acelera hasta alcanzar la velocidad de
propagación, su campo eléctrico llega a ser nulo y toda la energía potencial estará en su
campo magnético.
8.3. Modificación de las leyes electrodinámicas.
Como consecuencia de la demostración anterior deberemos modificar algunas de las
leyes que rigen las fuerzas eléctricas y las fuerzas magnéticas cuando las cargas
eléctricas tienen movimiento respecto al éter.
Esta modificación supone un paso adelante en la evolución de la electrodinámica clásica,
mientras que la interpretación que nos propone la Relatividad Especial supone la
destrucción de los principios básicos de la Física y de la Lógica.
Seguidamente presentaremos las leyes clásicas que quedan afectadas, y para facilitar su
expresión, al factor de eficacia lo designaremos con la letra griega Ψ (psi).
El factor Ψ tiene el valor inverso del factor γ de la Relatividad Especial. Para generalizar
las leyes sustituiremos la velocidad constante de la luz c por la velocidad de propagación
u.
En todas las leyes utilizaremos el mismo sistema de unidades: u.e.s.
v2
Factor de eficacia eléctrica:
ψ=
(8.3.1)
√1-u2
q
Intensidad del campo eléctrico:
E=
ψ
(8.3.2)
r2
Magnitud de la fuerza eléctrica:
F=Eqψ
(8.3.3)
q1q2ψ1ψ2
Ley de Coulomb dinámica:
F=
(8.3.4)
r2
vqsenθ
Intensidad del campo magnético:
H=
(8.3.5)
r2u
Hvqψ senθ
Magnitud de la fuerza magnética:
F=
(8.3.6)
u
8.4. La velocidad crítica.
La Relatividad Especial postula que existe una velocidad límite para el movimiento de los
cuerpos y este límite es la velocidad de la luz, la cual es considerada como una magnitud
constante (c).
En esta teoría del éter ya hemos demostrado que la velocidad de propagación no tiene un
valor constante, sino que depende de la densidad del éter que a su vez es variable.
En principio no hay ninguna razón para poner un límite a la velocidad del movimiento de
los cuerpos, la cual puede tener cualquier valor. Sin embargo existe una limitación real
para acelerar las partículas con carga eléctrica a una velocidad que alcance o supere la
propia de la propagación de las ondas electromagnéticas (u) puesto que según hemos
explicado en la sección 8.3. las fuerzas resultantes sobre una carga móvil son:
2
v
v2
o bien
senθ
F=Eq√1-u2
F=Hvq√1-
u2
y por consiguiente cuando v alcanza el mismo valor que u la fuerza resulta nula y no
puede ser acelerada la partícula.
Por otro lado, si se supera la velocidad de propagación correspondiente al éter, debido al
campo gravitónico de la propia partícula se origina una fuerza que tiende a frenarla hasta
que su velocidad sea igual a la de propagación. Este fenómeno será tratado en la sección
9.3.
No obstante es posible acelerar una partícula en un medio con una velocidad de
propagación específica y seguidamente hacerla pasar a otro medio con una velocidad de
propagación más pequeña con lo cual se habrá sobrepasado la velocidad de propagación
del segundo medio. Esto no es un experimento imaginario, pues corresponde al fenómeno
conocido como “radiación de Cerenkov” en el cual los electrones son acelerados hasta
una velocidad próxima a la de la luz y después se les hace pasar a un medio con
velocidad de propagación menor. Los electrones resultan frenados en el segundo medio y
producen una radiación que se puede observar.
En el espacio astronómico se pueden producir casos de superación de la velocidad
crítica, cuando un cuerpo con alta velocidad se interna en alguna región en donde la
densidad del éter es mucho mayor que en la región de origen. Recordemos que en las
inmediaciones de las estrellas de gran masa el éter puede alcanzar densidades muy altas.
Otro caso en el cual se supera la velocidad crítica es el conocido como “Bremsstrahlung”,
que se produce cuando un electrón de alta velocidad es acelerado por el campo eléctrico
de un núcleo positivo y penetra en la región de dominio gravitónico, donde la densidad del
éter puede alcanzar valores muy altos.
Por consiguiente podemos afirmar que no existe una velocidad límite para el movimiento
de la materia en el espacio vacío, pero sin embargo existe una velocidad crítica que
corresponde a la velocidad de propagación de las ondas en el éter, en la cual se producen
unos efectos especiales.
8.5. Algunas consecuencias de las nuevas leyes.
a) Puesto que no se produce un incremento de la masa al aumentar la velocidad y
además resulta posible que un cuerpo alcance la velocidad de propagación propia del
éter, una masa que se mueva a esta velocidad tendrá una energía cinética que estará de
acuerdo con las leyes de la mecánica clásica.
Según los postulados de la Relatividad Especial, la energía de una masa moviéndose a la
velocidad de la luz resultaría infinita y como esto es imposible, propone que es imposible
que una masa pueda alcanzar la velocidad de la luz. Sin embargo la luz tiene esta
velocidad y además los fotones tienen masa. ¿Cómo se puede explicar esta
contradicción? ¿Son los fotones la realización de algo imposible?
b) Otra consecuencia de las nuevas leyes es que si varias cargas eléctricas viajan a la
velocidad de propagación no se producirá ninguna fuerza entre ellas, como se desprende
de las ecuaciones 8.3.3 y 8.3.6 puesto que cuando v=u resultará que Ψ=0 y por
consiguiente la fuerza eléctrica y la fuerza magnética serán nulas. Sin embargo se
mantendrá la fuerza coeléctrica en el contacto absoluto entre las partículas.
c) Las velocidades se suman vectorialmente, de acuerdo con la mecánica clásica; por
consiguiente es posible superar la velocidad crítica con facilidad si el cuerpo en
movimiento y el medio de propagación tienen velocidades en sentido contrario.
d) También se supera la velocidad crítica si se acelera una partícula en un medio con una
determinada velocidad de propagación y después se le hace penetrar en otro medio con
menor velocidad de propagación, como sucede en el “efecto Cerenkov”.
e) En las proximidades de los núcleos atómicos la densidad del éter es muy alta y por lo
tanto la velocidad de propagación es muy baja, por lo cual es fácil superarla, como
suceden en el Bremsstrahlung.
f) La costumbre de expresar la energía de las partículas en electrón-voltios resulta
incorrecta, puesto que la velocidad alcanzada no es proporcional a la diferencia de
potencial, excepto a pequeñas velocidades. La forma correcta de expresar la energía de
las partículas es utilizar las unidades de la física clásica:
1
U=
mv2
2
g) La elevadísima energía cinética que se les achaca a las partículas muy aceleradas es
un error, por la misma razón que es erróneo considerar que la masa de estas partículas
ha aumentado con la velocidad.
Conocemos la inercia como una propiedad de la materia que se manifiesta como una
fuerza que tiende a oponerse a cualquier variación en el movimiento de un cuerpo.
También conocemos la relación que existe entre esta fuerza y la aceleración del
movimiento de una masa, que es F=ma.
La inercia es una propiedad fundamental de la materia y sobre ella se soportan los
principios básicos de la mecánica, como son la conservación de la energía, la
conservación de la cantidad de movimiento, la evaluación de la energía, etc. Sin embargo
se podría afirmar que de esta propiedad tan importante sabemos muy poco.
La fuerza de la inercia y la fuerza gravitatoria dependen ambas de la magnitud de la
masa. En nuestro entorno ambas fuerzas son proporcionales a la magnitud de la masa,
aunque ambas fuerzas corresponden a fenómenos bien diferenciados.
El convencimiento de que la masa gravitatoria y la masa inercial eran siempre
proporcionales a la fuerza llevó a Einstein a proponer su “principio de equivalencia entre
una aceleración y un campo gravitatorio”.
En esta teoría del éter se demostrará que no existe tal equivalencia, aunque se confirma
que la fuerza inercial y el campo gravitatorio son dependientes de la magnitud de la masa.
Anteriormente hemos demostrado que la fuerza gravitatoria, la fuerza eléctrica y la fuerza
magnética a distancia, se producen a causa de la fuerza coeléctrica que actúa por el
contacto directo entre la materia y el éter. Estos hechos nos inducen a preguntar: ¿tiene el
éter algún efecto sobre la inercia?, ¿podemos diferenciar la masa inercial de la masa
gravitatoria?
Estas dos preguntas tendrán una respuesta afirmativa en las siguientes secciones.
9.2. Relación entre la inercia y el éter.
Para demostrar la relación que existe entre la inercia de una masa y el éter que la rodea,
analizaremos lo que ocurre cuando un fotón que se desplaza a través del éter se interna
en el interior de un vidrio, donde sabemos que existe éter con una densidad mayor, por lo
cual tiene un índice de refracción n que es mayor que la unidad.
En la fig. 9.2.1 se representa el caso que vamos a tratar, en el cual un fotón que viaja a la
velocidad c se interna en un vidrio con índice de refracción n donde viajará a la velocidad
c
u=
n
En este proceso no se produce reflexión alguna.
h
c
u
ρa
ρ
fig. 9.2.1
Sabemos que la energía total del fotón es U=mc2
La velocidad de propagación obedece a la ecuación 7.2.3, que es:
Y
u=√
ρ
Y
donde
es la densidad de nuestro éter
que aplicada a nuestro entorno será c=√a
ambiental.
c
El índice de refracción está definido por n=
por lo cual:
u
Y
c
√ρa
ρ
c
n=
=
luego
n2 =ρ
y
u=
u
ρa
n
Y
=√ρa
√
ρ
La energía del fotón viajando por el espacio exterior debe ser la misma que cuando se
desplaza en el interior del vidrio, a pesar de que haya cambiado su velocidad, lo cual se
confirma porque al salir de nuevo al exterior mantiene su velocidad y su energía iniciales.
Para mantener la misma energía habiendo cambiado su velocidad, es necesario que la
masa inercial también haya cambiado. Tendremos:
2
mu
c
mu
Uc=Uu; mc c2=muu2; mc c2=mu
; mc=
;
=n2
n2
n2
mc
mu
ρ
donde
n2=ρ
por lo cual resulta
=
(9.2.1)
ρa
mc
ρa
Este resultado demuestra que la masa inercial es proporcional a la densidad del éter. Por
consiguiente la masa inercial es diferente de la masa gravitatoria, puesto que la primera
depende de la densidad del éter mientras que la masa gravitatoria es una magnitud
constante.
Esta diferencia nos obliga a identificar la masa inercial con un símbolo distinto de la masa
gravitatoria, por lo cual designaremos a la masa inercial en adelante usando una M y
reservaremos para la masa gravitatoria la letra minúscula m.
M = masa inercial
m = masa gravitatoria
En nuestro entorno la magnitud de la masa gravitatoria y la masa inercial es la misma,
porque las leyes establecidas se han basado en la misma cantidad de masa, adaptándose
a estas leyes los factores de proporcionalidad.
Ma = m cuando
Sin embargo cuando la densidad del éter sea diferente a la densidad de nuestro entorno,
que designaremos como
la masa inercial y la masa gravitatoria estarán en la siguiente
relación, respetando la ecuación 9.2.1.
ρ
M=m
(9.2.2)
ρa
Consecuentemente la relación entre fuerza y aceleración deberemos expresarla así:
F = Ma
(9.2.3)
En general deberemos usar el símbolo M para indicar la masa inercial, pero muy
especialmente en aquellos casos en los que sabemos que la densidad del éter difiere de
como sucede en las proximidades de las partículas subatómicas debido al campo
gravitónico, o en el entorno de los astros a causa del campo gravitatorio.
El hecho de que la masa inercial dependa de la densidad del éter además de justificar la
conservación de la energía de los fotones, tiene una gran trascendencia porque afecta de
modo importante a las órbitas de los electrones, así como también explica el corrimiento
de frecuencias del espectro de radiación de las estrellas, que ha sido observado por los
astrónomos.
La disminución de las frecuencias observadas en las estrellas de gran masa obedece a
que el éter que rodea estas estrellas tiene una densidad muy alta, lo que ocasiona un
incremento de la masa inercial, que a su vez dará lugar al retardamiento en el proceso de
radiación.
No es necesario recurrir a la “dilatación del tiempo” para explicar el fenómeno del
corrimiento de la frecuencia. Lo que sucede es simplemente que los procesos se hacen
más lentos, porque la inercia de la masa es mayor cuando el éter tiene mayor densidad.
Un reloj cualquiera situado en un lugar donde la densidad del éter sea mayor que la
densidad de nuestro éter ambiental, marchará más despacio. Lo mismo sucederá con los
procesos atómicos, que se desarrollarán con mayor lentitud. Si la densidad fuera menor el
reloj adelantaría.
El tiempo debe considerarse como una magnitud absoluta, como era considerado en la
física clásica, sin que por ello encontremos contradicciones. ¡Deberemos devolver al
tiempo lo que le pertenece!
La consideración del nuevo concepto de la masa inercial en la Astronomía o en la
Cosmología, puede facilitar la comprensión de muchos fenómenos que resultan difíciles
de interpretar y que actualmente se calculan mediante las leyes de la Relatividad General,
pero que no tienen un fundamento razonable.
9.3. Explicación del efecto del éter sobre la inercia.
El efecto que produce la densidad del éter sobre la masa inercial puede ser explicado
considerando las fuerzas coeléctricas que se producen por el contacto de las partículas
de masa con el éter circundante, como haremos a continuación.
Una partícula de masa, en estado de reposo respecto al éter, creará en su entorno un
incremento en la densidad del éter, por lo cual la densidad de éste en la superficie de la
partícula tendrá un valor de acuerdo con la ecuación 4.2.3 que será:
K3m
ρ=ρb +
r3
Si la partícula se desplaza en el éter con velocidad constante, el gradiente de densidad
acompañará a la partícula manteniendo la misma distribución de densidad que en estado
de reposo.
La fuerza coeléctrica que se produce sobre una superficie viene dada por la ecuación
2.3.1:
F=K1ρ1ρ2 A
Considerando un elemento de superficie dA tendremos:
dF=K1 ρ1 ρ2dA
En el caso del contacto entre una masa con densidad
y del éter con densidad
tendremos:
K3m
K3m
dF = K1 ρm ρe dA
donde ρe= ρb +
luego
dF=K1 ρmdA (pb+
)
r3
r3
Si la partícula de masa se encuentra en reposo con relación al éter o mantiene un
movimiento uniforme, la fuerza resultante de sumar vectorialmente las fuerzas
elementales será nula, ya que estas fuerzas están perfectamente equilibradas, tal como
se muestra en la figura 9.3.1.
v
→
df
df m
Fi=∑ df=0
fig. 9.3.1
Fi = 0
Sin embargo, cuando la partícula está sometida a una aceleración, debido a que la
alteración de densidad se propaga a una velocidad determinada en el éter que rodea la
partícula, la densidad en el éter de la superficie frontal quedará disminuida mientras que
en la parte posterior resultará aumentada, dando lugar a un desequilibrio de fuerzas, de
modo que la suma vectorial de las fuerzas elementales resulta una fuerza que tiene un
sentido contrario a la aceleración, como muestra la fig. 9.3.2.
Fi
Fi = ∑ df
→
df
Fi=∑ df
df
a
m
df
fig. 9.3.2
9.4. Superación de la velocidad crítica.
Anteriormente hemos afirmado que la densidad del éter que rodea una partícula mantiene
una distribución equilibrada cuando la partícula tiene una velocidad constante. Esto es
cierto mientras no se supere la velocidad crítica que es la velocidad de propagación de las
ondas gravitatorias, pero dejará de cumplirse al sobrepasar dicha velocidad.
Cuando la velocidad de la partícula es mayor que la velocidad de la onda gravitatoria, esta
no puede extenderse por delante de la partícula y por consiguiente no puede alcanzarse
una condición de equilibrio, por lo que el resultado de sumar vectorialmente las fuerzas
elementales dF será una fuerza con sentido contrario al movimiento de la partícula, tal
como se representa en la fig. 9.3.3.
Fi
Fi = ∑ df
df
df
v > u
m
df
fig. 9.3.3
Esta fuerza frenará la velocidad de la partícula hasta que ésta quede al mismo valor que
la velocidad de propagación de las ondas gravitatorias.
La existencia de una velocidad crítica tiene gran trascendencia porque permite explicar los
fenómenos ópticos bajo el concepto de partículas en movimiento, tal como proponía
Newton y como veremos en el capítulo 11.
NUEVO CONCEPTO DEL ELECTRÓN
10.1. Unas dudas justificadas.
Actualmente se tiene la certeza de que la emisión de fotones se origina en los átomos,
cuando los electrones que giran en torno a los núcleos pasan de unas órbitas a otras con
menor energía y también se sabe que una carga eléctrica acelerada produce una
radiación electromagnética, que es un componente esencial de los fotones. Sin embargo
resulta imposible explicar la emisión de fotones sin encontrar graves contradicciones o
recurrir a conceptos imaginarios sin una explicación razonable.
El primer avance para explicar este fenómeno lo hizo Niels Bohr, a quien siguieron otros
científicos que han desarrollado la moderna “mecánica cuántica” que nos ofrece una
interpretación matemática apoyándose en principios hipotéticos. No obstante estos
principios en unos casos son contradictorios y en otros casos son una pura abstracción
sin explicación concreta.
¿Por qué no radian los electrones en las denominadas órbitas permitidas o estacionarias?
Según las leyes electrodinámicas, deberían generar ondas electromagnéticas en
cualquier órbita.
¿Por qué no emiten ondas gravitatorias en ningún caso?
¿Por qué tiene el electrón una carga eléctrica opuesta en signo, pero de igual magnitud
que el protón, mientras su masa es 1.836 veces más pequeña?
¿Cómo son los electrones?
A juicio del autor, la dificultad para dar respuesta a estas preguntas tiene su origen en el
hecho de haberse concebido un concepto equivocado del electrón. Desde que fue
descubierto el electrón se lo ha imaginado como una partícula simple que tiene carga
eléctrica y masa. Posteriormente se ha puesto en duda su constitución y se ha convertido
en un ente indescriptible.
Seguidamente vamos a proponer un nuevo concepto de los electrones que estará de
acuerdo con las leyes electrodinámicas.
10.2. El electrón filiforme.
Hasta ahora se ha considerado el electrón como una pequeña partícula que gira en torno
a los núcleos atómicos y que además puede viajar libremente al separarse de los átomos.
No existe ninguna razón especial que nos obligue a pensar que debe ser así y
probablemente esta idea ha sido sugerida por el ejemplo que nos dan los planetas
girando alrededor del sol, o los satélites girando alrededor de un planeta, pero nadie se ha
acordado del planeta Saturno con sus anillos circundantes.
La electrodinámica nos enseña que una carga eléctrica acelerada produce una radiación
electromagnética, pero también nos demuestra que una corriente constante en un circuito
cerrado no produce radiación alguna, a pesar de que las cargas eléctricas que constituyen
la corriente sufren una aceleración.
Ello se debe a que el campo electromagnético originado por la aceleración en un punto
del circuito queda anulado por la integración de los campos procedentes del circuito
completo. Pero bastará con que la corriente sufra una variación, para que no se produzca
la anulación de los campos y tenga lugar la radiación correspondiente.
I
fig. 10.2.1
Por consiguiente, si los electrones están constituidos por cargas eléctricas elementales
dispuestas en forma de anillo que gira en torno al núcleo, según muestra la fig. 10.2.2. no
se producirá ninguna radiación mientras la corriente equivalente sea constante, a pesar
de que cada elemento de carga sufre una aceleración centrípeta al recorrer la órbita.
v
+P
-e
fig. 10.2.2
Esta configuración del electrón formado por una cadena de cargas negativas elementales
supone un primer paso, pero no es suficiente, porque una estructura semejante se
desintegraría espontáneamente debido a la repulsión que sufrirían entre sí dichas cargas.
La solución de este problema la tendremos si consideramos el concepto de las partículas
subatómicas que se expone en la sección 2.5. donde estas partículas se describen como
un agrupamiento de cargas eléctricas elementales de ambos signos, llamadas electrinos,
que se ordenan en forma de red cúbica y en el caso de partículas con carga neta, el
exceso de carga se sitúa en la superficie, confiriéndole el signo correspondiente.
Por otro lado sabemos que la masa del protón es 1.836 veces mayor que la del electrón,
mientras su carga eléctrica es la misma pero con signo opuesto. Esto es un valioso indicio
para deducir que su forma geométrica debe ser diferente, apoyándonos en la hipótesis de
que en ambos casos la superficie queda totalmente cubierta por la carga neta.
Si asumimos que el electrón extendido tiene la forma de un largo filamento, su superficie
corresponde a la de un cilindro, lo que nos permite calcular sus dimensiones con relación
a las del protón al cual consideramos con forma esférica. La fig. 10.2.3 representa las
dimensiones del protón y del electrón que deseamos comparar. Si la superficie del protón
y del electrón están saturadas de electrinos, debido a que la carga eléctrica de ambos es
de la misma magnitud, se deduce que la superficie también será igual:
S p= Se luego
4 πR2=2 πrℓ
Protón
l
r
fig. 10.2.3
Electrón extendido
4
El protón con forma esférica tiene un volumen:
πR3
Vp=
3
El electrón extendido es un cilindro con volumen:
Ve=πr2 ℓ
Para la misma densidad de masa, el protón deberá tener un volumen que sea 1.836
veces mayor que el volumen del electrón:
4
luego
πR3 = 1.836 πr2 ℓ
Vp=1.836Ve
3
Como las superficies deben ser iguales podemos determinar cual será la longitud del
electrón respecto al radio del protón:
4
πR3=1. 836 πr2 ℓ ; R3=1 . 377 πr2 ℓ
3
2
4 πR2=2 πrℓ ; 2 R2=rℓ ; r=2R
ℓ
2
2
luego
ℓ = 5.5.08R ;
R3 = 1.377 (2Rℓ
)ℓ;R3=5.508R4
ℓ
Por consiguiente, las dimensiones del electrón respecto al radio R del protón serán:
ℓ=5.508 R
(10.2.1)
R
El radio del filamento será:
r=
(10.2.2)
2.754
La relación entre la longitud del electrón y el radio de su filamento será:
ℓ
=15.169.032
(10.2.3)
r
Este resultado nos indica que el electrón es un filamento con un diámetro pequeñísimo
respecto a su longitud.
La longitud calculada corresponde al caso en el que el electrón ocupa la órbita más
pequeña posible, pero su constitución le permite alargarse cuando por una causa externa
incrementa su energía obligándole a realizar órbitas de mayor radio, según se demostrará
en la siguiente sección.
Actualmente se estima que el radio del protón es aproximadamente de 1,4 x 10-15 m
, lo
que nos permite calcular el radio de la órbita mínima que pueden ocupar los electrones,
que designaremos como R1:
-15
ℓ
5.508R
5.508x1,4x10
R1=
=
=
=1,227x 10-12m
2π
2π
2π
Observamos que este valor es menor que el ofrecido por la teoría de Bohr que es
R=53x10-12m.
Esta diferencia podría ser explicada porque en la teoría de Bohr y en las estimaciones del
radio de los protones no se han considerado los efectos que habrían de producirse si se
aplicaran algunos de los postulados de esta teoría del éter como son los siguientes :
Existencia de una fuerza gravitónica en la proximidad del núcleo (Sección 4.2.).
Aumento de la masa inercial por la mayor densidad del éter (Sección 9.2.).
Disminución de la fuerza eléctrica al aumentar la velocidad (Sección 8.2.).
Cuando se descubrió que en las órbitas de menor radio los electrones no emitían con la
frecuencia que correspondía a su frecuencia de rotación, Bohr propuso un principio que
se conoce como “Principio de correspondencia” y que dice lo siguiente: en el límite de las
órbitas grandes y energías elevadas, los cálculos cuánticos deben coincidir con los
clásicos.
Este principio que fue concebido para justificar la diferencia entre los resultados
experimentales y los esperados de aplicar las leyes clásicas, no tenía entonces ninguna
justificación razonable. Es la existencia del campo gravitónico en las proximidades de los
núcleos lo que puede justificar los resultados experimentales, aunque en este momento
no podamos hacer una valoración cuantitativa por carecer de datos numéricos suficientes.
10.3. Órbitas estacionarias.
Para poder explicar la existencia de ciertas órbitas privilegiadas, en las cuales el electrón
no radia, mientras que en otras si lo hace, deberemos describir con más detalle la
estructura del electrón.
En primer lugar deberemos asumir que sus componentes, las cargas eléctricas que
denominamos electrinos, no están ligados entre sí de forma rígida, sino que disponen de
la movilidad necesaria para que el electrón pueda adaptarse a la longitud de la órbita
correspondiente a una determinada energía.
El núcleo del electrón, que consiste en un filamento constituido por electrinos de ambos
signos, presenta en su superficie cilíndrica los electrinos ordenados de modo alternativo
respecto a su signo, tal como ilustra la fig. 10.3.1.
-
-
-
-
-
-
+ -+
-
+
-
-
+
-
+
-
+
-
+
-
fig. 10.3.1
-
-
-
-
-
Los electrinos negativos que constituyen la carga neta del electrón, ocupan la superficie
del filamento, situándose cada uno en contacto con un electrino positivo del núcleo.
La carga negativa superficial del electrón solamente satura la superficie del mismo, en el
caso correspondiente a la longitud mínima, que es el caso de la órbita normal o sin
excitar.
Sin embargo, en un electrón excitado por haber recibido un aporte de energía exterior, su
longitud aumentará por haber pasado a una órbita de mayor radio, lo cual obligará a las
cargas superficiales a distribuirse de nuevo, enfrentándose siempre con los electrinos
positivos del núcleo, pero ahora sin ocupar todos los huecos.
Cuando la nueva distribución resulte uniforme, el electrón se encontrará en una órbita
estable, pero si la distribución no es perfectamente uniforme se producirá una radiación
electromagnética de acuerdo con las leyes electrodinámicas.
Seguidamente vamos a determinar cuales son las condiciones necesarias para que la
carga neta del electrón quede uniformemente repartida en toda la longitud del filamento
electrónico.
En la fig. 10.3.2 se muestran las posiciones que los
electrinos de la carga superficial deberán ocupar
sobre el núcleo del electrón cuando éste aumenta su
σ1
longitud.
La carga neta del electrón es una cantidad constante
(q) que produce una densidad de carga superficial
que es:
σ1
q
σ=
2
A
Debido a que las cargas elementales, los electrinos,
no se fraccionan, la disminución de densidad solo se
produce con uniformidad cuando se realice por
σ1
fracciones enteras de
1
, como:
3
σ1
σ1
σ1
σ1
;
;
;
2
3
4
N
fig. 10.3.2
Donde N debe ser un número entero cualquiera. Puesto que la carga neta permanece
constante en el proceso de alargamiento, el área superficial deberá multiplicarse por el
factor entero N:
AN=A1 N
Además el volumen del núcleo cilíndrico deberá permanecer constante al alargarse el
electrón:
Ar
V=
=πr2 ℓ= constante
2
Donde A=superficie cilíndrica, r=radio del cilindro, l=longitud.
Para que se mantenga constante el volumen del cilindro cuando su superficie se multiplica
por N, el radio del cilindro deberá quedar dividido por el mismo factor, de modo que
tendremos:
NA
2
1
N2ℓ1
(rN )=π(rN )
2
Donde NA1=An es la superficie del electrón excitado y N 2
1 =
N es la longitud del mismo.
Por consiguiente podemos afirmar que un electrón solo podrá mantenerse en una órbita
estacionaria, sin emitir una radiación, cuando su longitud corresponda a:
ℓN =N2ℓ1
(10.3.1)
Donde
es la longitud en la órbita mínima y N es un número entero. Puesto que en una
órbita circular
, podemos determinar el radio R de las posibles órbitas
estacionarias:
ℓN =N2ℓ1; 2πRN=N22πR1
luego
RN=N2 R1
(10.3.2)
La ecuación 10.3.2 es la misma que ofrece la teoría de Bohr, pero ahora hemos llegado
hasta ella sin apoyarnos en hipótesis que contradicen las leyes de la electrodinámica, ya
que nos hemos basado en unos principios razonados que están plenamente de acuerdo
con la electrodinámica clásica.
Por otro lado hemos podido definir de una forma concreta lo que es un electrón, el cual
últimamente resultaba un elemento indescriptible.
Deberemos advertir que las demostraciones anteriores son una simplificación de la
realidad, porque hemos eludido considerar la pequeña variación de masa que debe sufrir
el electrón cuando absorbe o emite un fotón.
10.4. Emisión de fotones.
Cuando la distribución de la carga eléctrica sobre la superficie del electrón no resulte
uniformemente repartida, se producirá una radiación electromagnética al mismo tiempo
que emitirá una parte de su masa en forma de fotones, perdiendo la energía
correspondiente y pasando a una órbita estacionaria de menor energía. En sentido
inverso, cuando el electrón absorbe un fotón deberá aumentar su masa y energía.
La carga neta del electrón no deberá disminuir en el proceso de la emisión de un fotón,
por lo cual es necesario que la masa del fotón emitido esté constituida por electrinos de
ambos signos en la misma cantidad.
Los nuevos conceptos expuestos anteriormente sugieren la posibilidad de desarrollar una
teoría sobre la mecánica de los átomos y la radiación de fotones, sustituyendo los
hipotéticos principios de la mecánica cuántica por unos principios razonados que además
están de acuerdo con las leyes clásicas de la electrodinámica.
Esta tarea resulta de una gran complejidad que excede las pretensiones de este trabajo y
de la capacidad del autor, por lo que consideramos que es un interesante desafío para
aquellos especialistas capaces de llevarla adelante, apoyándose en los siguientes
principios:
1.- Los electrones tienen forma de anillo y se componen de electrinos. (10.2.)
2.- Las órbitas de los electrones solo son estables cuando su carga neta está
uniformemente distribuida sobre la superficie del electrón. (10.3.)
3.- Los electrones que no cumplen las condiciones de una órbita estable emitirán una
radiación electromagnética al mismo tiempo que un fotón. (7.6.)
4.- La masa de los fotones procede de los electrones. (10.4.)
5.- La velocidad de propagación de las ondas electromagnéticas y de los fotones
depende de la densidad del éter, que a su vez depende de la distancia al núcleo del
átomo. (4.2.)
6.- La masa inercial depende de la densidad del éter. (9.2.)
7.- La fuerza eléctrica es función de la velocidad. (8.3.)
8.- La fuerza gravitónica es función de las masas y de la distancia. (4.2.)
El fenómeno de la luz, esa maravilla que nos permite ver con claridad todo lo que nos
rodea es sin embargo el fenómeno que más dificultad ofrece cuando intentamos conocer
su naturaleza verdadera, habiendo llegado hasta nuestros días sin que todavía tengamos
una explicación satisfactoria.
Uno de los aspectos más desconcertantes se debe al hecho de que en algunos casos se
comporta de acuerdo con los fenómenos ondulatorios, mientras que en otros casos sigue
las leyes de las partículas en movimiento.
La física moderna ha creado el fotón, que es un intento para superar el problema de esta
dualidad de comportamiento, pero todavía no se ha podido hacer una definición concreta
del mismo.
El motivo de esta dificultad obedece principalmente a que han sido asumidos algunos
conceptos falsos introducidos por la Relatividad Especial y por la Mecánica Cuántica.
Estos conceptos han bloqueado la posibilidad de profundizar en el conocimiento de la
naturaleza de la luz y será necesario, antes de desarrollar una teoría sobre la misma,
despejar todos los errores asumidos.
11.2. Los falsos postulados.
El primer postulado falso aceptado en la física moderna es el de la propagación de las
ondas electromagnéticas en el vacío absoluto.
Este fenómeno ya ha sido explicado en el capítulo 7 como una propagación del
movimiento de rotación de los eterones en el éter, el cual actúa como medio de
transmisión.
Otro postulado falso es la constancia de la velocidad de la luz en el vacío. También hemos
demostrado que esta velocidad es relativa al medio de propagación y que su magnitud
depende de la densidad del éter que no es constante, sino que depende de la influencia
de las masas.
El incremento de la masa con el aumento de la velocidad es otro error de la mayor
importancia. En el capítulo 8 hemos demostrado que el aparente crecimiento de la masa
queda justificado por una disminución de la fuerza eléctrica.
Este error tiene como consecuencia que la Relatividad Especial se vea obligada a
considerar nula la masa de los fotones en reposo, pues de no ser así nos encontraríamos
ante el increíble resultado de que un fotón con la velocidad de la luz tendría una masa
infinita, como se demuestra seguidamente:
v2
Siendo
m=m
v=c;
m=mo∞
o
/√1-c2 ;
Según la teoría del éter, la masa no varía con la velocidad y por lo tanto si adjudicamos
una masa determinada a los fotones que viajan a la velocidad de la luz, deberemos
aceptar que ese valor de la masa deberá mantenerse cuando se encuentre en reposo.
Por consiguiente un fotón puede depositar su masa en alguna otra partícula, además de
transferirle su energía.
Por último vamos a demostrar que también es falsa la interpretación de que la energía de
los fotones se debe únicamente a la energía cinética de su masa, que según la ecuación
relativista es:
E = mc2
mientras que según la mecánica clásica debería ser:
1
E=
mc2
2
Esta demostración resulta bastante extensa y tiene una importancia muy grande, por lo
cual requiere que se le dedique una sección completa.
11.3. Energía de los fotones.
Las leyes de la mecánica clásica permiten calcular la fuerza media que se produce
cuando un chorro de partículas de intensidad constante incide sobre una superficie con
choque inelástico.
En cada partícula tendremos:
t2
mv=∫ Fdt = Fm Δt ; Fm =mv
Δt
t1
En un chorro de partículas resulta:
∑mv
Mv
Fm=
=
Δt
Δt
donde M es la masa total que ha incidido durante el intervalo de tiempo
, de acuerdo
con la fig. 11.3.1.
F
F
Fm
fig. 11.3.1
∆t
Cuando el choque es perfectamente elástico, las partículas incidentes son reflejadas en
sentido contrario, lo cual determina que en un chorro de partículas como en el caso
anterior, la fuerza resultante tenga un valor doble:
2 Mv
Fm =
Δt
Si designamos la fuerza media en choque inelástico como Fi y en choque elástico como
Fe tendremos:
Mv
2Mv
Fi =
Fe=
Δt
Δt
Podemos determinar la relación existente entre la potencia de un chorro de partículas y la
fuerza media que produce su impacto sobre un blanco.
La potencia media desarrollada en un sistema se define como la cantidad de trabajo
producido en la unidad de tiempo y también como la cantidad de energía intercambiada
en la unidad de tiempo:
W
E
P=
P=
Δt
Δt
1
Como la energía es E=
mv2 tendremos una potencia que será:
2
2
E
Mv
P=
=
luego
Mv2 =2 ΔtP
Δt
2 Δt
El impulso recibido en el intervalo de tiempo
será:
2ΔtP
2E
p= Mv =
que también es
p=
v
v
En un choque inelástico o absorbente resultará una fuerza:
Mv
2P
Fi =
=
Δt
v
mientras que en un choque perfectamente elástico la fuerza será:
2Mv
4P
Fe=
=
Δt
v
En la práctica el choque es parcialmente elástico y absorbente, por lo cual deberemos
considerar el coeficiente de reflexión β que puede variar desde 0 hasta 1 según las
características del material reflector utilizado. La fuerza en este caso será la suma de una
parte con reflexión total y de otra parte con absorción total:
4 Pβ
2P(1-β)
2P(1+β)
F=Fe+Fi
F=
+
=
v
v
v
Aplicando este resultado a un rayo de luz con v=c resulta:
2P(1+β)
F=
c
Se han realizado numerosos experimentos para determinar la presión de radiación, entre
los cuales destacan los de Nichols y Hull. Posteriormente se han realizado con mayor
precisión en el año 1923 por Gerlach y Golsen.
Estos experimentos se basaban en la medida de la fuerza ejercida por un rayo de luz de
potencia conocida, sobre una lámina con un coeficiente de reflexión específico, que
estaba suspendida en el vacío.
El resultado de los experimentos realizados concuerda con una precisión del 2% con la
ecuación siguiente:
P(1+β)
2P(1+β)
F=
en lugar de corresponder a
F=
c
c
como debería ser de acuerdo con la dinámica clásica.
Este resultado condujo a la conclusión de que la cantidad de movimiento de los fotones
debía ser:
E
2E
p=
en lugar de
p=
c
c
Esta interpretación del resultado experimental es errónea, como vamos a demostrar a
continuación.
El error tiene su origen en considerar que la energía de un fotón reside únicamente en la
energía cinética de su masa, además de que es equivocado pensar que una onda que
incide sobre una superficie pueda producir una fuerza media apreciable cuando el
intervalo de tiempo considerado es grande respecto al periodo de la onda.
Se puede demostrar que la fuerza media producida por cualquier modalidad de onda
sobre una superficie resulta nula, pues aunque se produzca una fuerza durante un
semiciclo de onda, en el semiciclo siguiente el sentido de la fuerza se habrá invertido y
por consiguiente el resultado de integrar estas fuerzas durante un tiempo grande respecto
a la duración de un ciclo, dará un resultado nulo mientras la amplitud de la onda se
mantenga constante.
La razón por la cual los experimentos realizados dan como resultado una fuerza cuyo
valor es la mitad del valor esperado, se debe a que la energía total de los fotones tiene
una componente cinética y otra componente electromagnética, siendo la energía cinética
la única que puede producir un impulso sobre el blanco.
Si la energía cinética de los fotones es la mitad de la energía total de los mismos,
tendremos:
1
2P(1+β)
P(1+β)
F=
luego
F=
2
c
c
lo cual está en perfecto acuerdo con el resultado de los experimentos y también con la
mecánica clásica.
Podemos afirmar que la energía de los fotones tiene dos componentes de igual valor. La
mitad es energía cinética transportada por la masa y la otra mitad es energía
electromagnética transportada por la onda asociada:
luego
E=mc2
E=2(12mc2)
Puede sorprender el hecho de que en la luz participen dos formas de energía con la
misma magnitud, pero no es la primera vez que encontramos esta circunstancia, pues
podemos recordar que la energía de la radiación electromagnética se compone por partes
iguales de la energía de un campo eléctrico y de la energía de un campo magnético.
No obstante, deberemos recordar que en último término, toda la energía de los fotones es
energía cinética, porque según quedó demostrado en la sección 6.8. la energía de los
campos electromagnéticos se debe al movimiento de rotación de los eterones, pero
mientras la energía de la masa de los fotones puede producir un impulso sobre la
superficie de impacto, la energía cinética de los eterones no participa en este impulso,
porque su movimiento es de rotación y además alternativo.
11.4. Naturaleza de la luz.
Una vez despejados los conceptos falsos que impedían una correcta interpretación de los
fenómenos observados con relación a la luz, estamos en disposición de acercarnos un
poco más al conocimiento de la misma, sin incurrir en contradicciones ni apelar a
conceptos inexplicables.
La luz no es únicamente una radiación electromagnética, sino que es una radiación
electromagnética asociada con partículas de masa que se desplazan a la velocidad de
propagación propia del éter.
No hay ninguna razón para pensar, como se ha hecho hasta ahora, que todas las
radiaciones participan de estas mismas propiedades y es razonable admitir que pueden
existir radiaciones electromagnéticas puras y radiaciones “fotónicas”.
En la primera clase estarán aquellas radiaciones que se generan fuera de los átomos por
el movimiento de cargas eléctricas a baja velocidad y que no alcanzan frecuencias muy
elevadas, como son las ondas de radio y las microondas.
En la categoría de radiaciones fotónicas se incluirán aquellas otras que se originan en los
átomos o en los electrones muy acelerados y que tienen frecuencias muy elevadas, tales
como rayos infrarrojos, luz visible, rayos ultravioleta, rayos X y rayos gamma.
El aceptar que los fotones incluyen realmente partículas con masa está en conformidad
con su naturaleza cuántica, lo que fue demostrado por Einstein en su conocido trabajo
sobre el efecto fotoeléctrico y que después confirmó Milikan.
Einstein comprobó que la luz era absorbida por otras partículas en cantidades discretas,
en vez de serlo de manera continua como era de esperar. Además la cantidad de energía
siempre es un múltiplo entero de una cantidad fija que denominó cuanto de luz o fotón y
cuya magnitud es:
E=hf
donde h es la constante de Planck y f es la frecuencia.
La energía de este cuanto de luz es independiente de la intensidad de la radiación
luminosa a la cual pertenece.
El efecto fotoeléctrico demuestra que los fotones no transportan carga eléctrica neta, lo
que significa que transportan una cantidad de masa constituida por cargas eléctricas
elementales en cantidad equilibrada. Por otro lado hemos demostrado en la sección 11.3.
que los fotones son portadores de una energía electromagnética del mismo valor que la
energía cinética de su masa.
También sabemos que la luz tiene propiedades de una onda eléctrica transversal y resulta
polarizada de acuerdo con el vector eléctrico de su campo electromagnético.
El efecto Zeeman demuestra que la luz se genera por los electrones que giran en torno al
núcleo de los átomos. Otros fenómenos como el “efecto Cerenkov” o el “bremsstrahlung”
también prueban que los electrones emiten luz cuando sufren una desaceleración.
El conocimiento de los fenómenos descritos, en unión con los principios establecidos en
esta teoría del éter, nos va a permitir que podamos hacer una descripción aproximada de
la naturaleza de los fotones, sin pretender que esta descripción explique todo lo que aún
falta por conocer acerca de los mismos.
11.5. Descripción aproximada de los fotones.
Las consideraciones hechas anteriormente nos conducen a establecer las condiciones
que deberá cumplir un fotón, que serán los siguientes:
a) Deberá contener una cantidad determinada de masa.
b) No puede tener carga eléctrica neta.
c) Deberá transportar un campo electromagnético transversal.
d) Deberá moverse a la velocidad de propagación de las ondas en el éter.
e) Si asumimos los postulados de la física moderna, la frecuencia de la onda
electromagnética asociada al fotón deberá estar de acuerdo con las siguientes
ecuaciones:
E= mc2; E=hf
donde h es la constante de Panck que equivale a 6,626x1027
ergios.
Ahora deberemos encontrar una estructura del fotón que cumpla con todas las
condiciones mencionadas.
Daremos un primer paso considerando un par de cargas eléctricas elementales, que ya
conocemos como electrinos, con carga de signos opuestos, los cuales se desplazan en el
éter a la velocidad de propagación de la luz, dispuestas según indica la fig. 11.5.1.
u
fig. 11.5.1
A este par de cargas asociadas lo denominaremos en adelante fotino. Bajo el concepto
del campo eléctrico de la electrodinámica clásica, este fotino no puede en ningún caso
generar un campo eléctrico, ni un campo magnético, debido a que las cargas eléctricas de
signos opuestos se neutralizan mutuamente cuando están reunidas.
Considerando la teoría del éter y de acuerdo con la modificación de la electrodinámica
expuesta en el capítulo 8, las cargas eléctricas desplazándose a la velocidad de
propagación tampoco pueden generar un campo eléctrico, pero sí generan un campo
magnético.
Este fotino desplazándose a la velocidad de propagación en el seno del éter da lugar a un
campo magnético estacionario que tiene unas características diferentes de las que
conocíamos hasta ahora, pero antes de analizarlo deberemos recordar algunos conceptos
que se han explicado en la sección 7.5.
1º.- Consideramos que un campo magnético estacionario H es en esencia el movimiento
de rotación de los eterones, que puede ser variable en el tiempo, pero los eterones
permanecen en el mismo lugar mientras giran.
2º.- El campo eléctrico radiado Er se produce cuando la aceleración rotacional de los
eterones provoca un desplazamiento transversal de la carga eléctrica. Este
desplazamiento avanza con la velocidad de propagación correspondiente a la densidad
del éter.
3º.- El campo magnético radiado Hr se origina como consecuencia del movimiento de
avance de la carga eléctrica desplazada y su magnitud es Hr=Er u de acuerdo con la
ecuación 7.5.2.
Al avanzar el fotino inmerso en el éter obligará a los eterones con los que toma contacto a
girar sobre sí mismos, con lo cual se genera un campo magnético estacionario que tiene
en todos los eterones el mismo sentido, como se representa en las fig. 11.5.2 y 11.5.3.
Este resultado difiere bastante del campo magnético que conocíamos hasta ahora, en el
cual el campo se genera por cargas eléctricas de un mismo signo y las líneas de flujo se
cierran formando círculos.
El campo magnético estacionario H tendrá la misma magnitud en cualquier dirección que
2uq
será:
H=
(11.5.1)
r2
donde q es la carga de un electrino.
u
fig. 11.5.2
u
fig. 11.5.3
En la fig. 11.5.4 se representan de forma idealizada las curvas de variación del campo
magnético estacionario H y del campo eléctrico radiado Er en función de la distancia al
fotino.
H
2uq
H =
r2
u
-r
+r
+Er
Er = (f)a
u
-r
+r
fig. 11.5.4
-E
r
Al avanzar el fotino en el éter, los eterones situados delante del mismo sufrirán una
aceleración positiva al crecer el campo magnético estacionario, lo cual dará lugar a un
campo eléctrico radiado de sentido positivo. Sin embargo en la parte posterior del fotino el
campo magnético tiene un valor decreciente, lo cual implica una aceleración negativa de
los eterones, lo cual dará lugar a un campo eléctrico radiado de sentido negativo.
Podemos determinar la magnitud del campo eléctrico radiado por el fotino que se
desplaza a la velocidad de propagación, aplicando las leyes de la electrodinámica:
dHr
Er=
u.e.s.
(11.5.3)
dtu2
Como el fotino se desplaza con velocidad u, el intervalo de tiempo dt puede ser expresado
en función de la distancia. De acuerdo con la fig. 11.5.5.
u
E
E
θ
E
θ
fig. 11.5.5
E
dr
dr=dtucosθ; dt=
ucosθ
Sustituyendo este valor de dt en la ecuación 11.5.3. obtendremos:
dHr cosθ
Er=
u.e.s.
(11.5.4)
dru
En la parte posterior del fotino, cosθ es negativo, por lo cual resulta E negativo.
De acuerdo con la ecuación 11.5.2. el campo magnético estacionario es:
2uq
dH
4 uq
H=
y por lo tanto
=
r2
dr
r3
que llevado en la ecuación 11.5.4 ésta se convierte en:
4qcosθ
Er=
u.e.s.
(11.5.5)
r2
Este campo eléctrico avanza en el éter acompañando al fotino, con lo cual se genera un
campo magnético radiado cuya magnitud según se demuestra en la sección 7.5. será:
Hr =Er u
u.e.s.
La dirección del campo eléctrico está en el mismo plano que ocupa el fotino y es
perpendicular a la trayectoria.
La dirección del campo magnético radiado es perpendicular a la del campo eléctrico y
también a la trayectoria del fotino.
El sentido de ambos campos deberá ser tal como se representa en la figura 11.5.6.
Er
Er
fig. 11.5.6
Una vez establecidas las características de un fotino, podemos pasar a definir lo que
puede ser un fotón, utilizando los fotinos como elementos constituyentes del mismo.
Sabemos que los fotones son portadores de una cantidad variable de masa y actualmente
está comprobado que su energía tiene un valor que es E=hf, donde h es la constante de
Planck y f es la frecuencia de la onda.
La primera característica que podemos adjudicar a los fotones es que son una ráfaga de
fotinos, tales como hemos definido anteriormente y que viajan por el éter a la velocidad
propia de las ondas electromagnéticas.
Para cumplir con el postulado de E=hf se hace necesario que la longitud de los fotones
sea de una magnitud constante, para conseguir que la energía transportada sea
proporcional a la frecuencia. Esa magnitud está aún sin determinar.
Por último será necesario que esta ráfaga de fotinos determine de algún modo los ciclos
que constituyen la onda, lo que ocurrirá si la cadena de fotinos adopta la forma de una
espiral tal como muestra la figura 11.5.7.
En la fig. 11.5.7 solo se representa la curva correspondiente al campo eléctrico radiado Er,
pero no se debe olvidar que en la misma fase que éste, se encuentra el campo magnético
radiado Hr, que tiene sentido perpendicular al mismo y también respecto a la trayectoria
del fotón. En este caso se han representado tres ciclos o periodos de onda, pero
deberemos considerar que de acuerdo con la frecuencia, quedarán incluidos más o
menos ciclos.
Er
u
Hr = Er u
λ
λ
λ
fig. 11.5.7
l
Cada fotino será portador de una energía que estará de acuerdo con su masa y la
velocidad de propagación siendo su magnitud:
E1=M1u2
La mitad de esta energía será cinética y la otra mitad será electromagnética. La energía del fotón
será la correspondiente a la totalidad de los fotinos incluidos:
E=Mu2
El hecho que los fotinos sean los portadores de la energía de los fotones es el causante
de la cuantización de los mismos, pero es un grave error considerar que todas las formas
de la energía están cuantizadas. No debemos extender a otros fenómenos una
característica que es peculiar de las radiaciones fotónicas.
Una propiedad de los fotones que los diferencia esencialmente de la radiación
electromagnética pura es que siempre mantienen la misma energía por mucho que se
alejen del punto de emisión, debido a que el producto mc2, que deberemos escribir Mu2, se
mantiene constante cuando se desplaza en el espacio.
La masa de los fotones también es la causante de que estos sean afectados por las
fuerzas de los campos gravitatorios, mientras su equilibrio eléctrico los hace insensibles a
los campos eléctricos y magnéticos.
11.6. Propagación de la luz.
Desde que Maxwell formuló sus ecuaciones sobre los campos electromagnéticos, se
aceptó que la luz consistía en ondas electromagnéticas y que su propagación obedecía a
las mismas leyes. Es bien conocida la ecuación que determina la velocidad de
propagación en función del coeficiente de permeabilidad magnética y de la constante
dieléctrica:
1
u=√
με
Cuando esta ecuación se aplica al espacio vacío en nuestro entorno resulta:
u=2,998 x 108 m/s =c
La Teoría de la Relatividad Especial postula que las ondas electromagnéticas se propagan
en el vacío absoluto y que su velocidad es constante. Además afirma que esta velocidad
es constante respecto al observador aunque éste se desplace con cualquier velocidad.
La teoría del éter rechaza este postulado y propone que la velocidad de la luz o de
cualquier radiación electromagnética se propaga con una velocidad relativa al éter y que
esta velocidad no tiene un valor constante, sino que depende de la densidad del éter que
a su vez es variable. En la sección 7.2. se demuestra que la velocidad de propagación es:
Y
(7.2.3)
u=√
ρ
En nuestro entorno la densidad del éter es ρa y por lo tanto tendremos:
Y
(11.6.1)
u=√a
que deberá tener el mismo valor que el adjudicado a la velocidad c.
En la actualidad no disponemos de los datos numéricos para determinar los valores de Y y
de ρa, pero no obstante esta ecuación resultará de gran utilidad para explicar algunos
fenómenos ópticos, como veremos más adelante.
11.7. Los cuerpos transparentes.
La experiencia demuestra que la luz se propaga con menos velocidad en los cuerpos
transparentes que en el espacio vacío. La relación entre estas velocidades determina el
índice de refracción (n) de un material transparente de modo que:
c
n=
(11.7.1)
u
Donde c es la velocidad en el vacío de nuestro entorno y u es la velocidad en el seno del
material.
La medida del índice de refracción de diversas sustancias demuestra que tiene una
dependencia de la densidad específica del material, pero no es una dependencia
exclusiva, pues la relación varía de unas sustancias a otras y además también varía con
la frecuencia de la luz.
La causa de la disminución de la velocidad dentro de los cuerpos transparentes es el
aumento de la densidad del éter en el interior de los mismos, debido al campo gravitónico
que existe en las proximidades de las partículas que constituyen el material, tal como se
explicó en la sección 4.4.
11.8. El arrastre de la luz por los cuerpos transparentes.
Cuando la luz se propaga dentro de un cuerpo transparente y éste se desplaza en la
misma dirección, la velocidad de la luz sufre una variación que es solo una fracción de la
velocidad del cuerpo:
Δu=αv
donde α es el coeficiente de arrastre y v es la velocidad del cuerpo.
Este arrastre parcial ha sido un fenómeno misterioso cuyas causas no eran conocidas,
aunque se pudo determinar su magnitud que es:
2
u
α=1-
c2
1
o también
α=1-
(11.8.1)
n2
Este valor fue confirmado por el famoso experimento de Fizcan, quien determinó el
arrastre de la luz por el agua que fluía en el interior de unos tubos, con una velocidad
conocida.
Ahora podemos dar una explicación razonada a este arrastre de la luz, basándonos en el
arrastre que sufre el éter por las masas en movimiento que fue tratado en el capítulo 4.
En la sección 4.5. se ha demostrado que una masa en movimiento origina en el éter un
incremento de densidad Δρ y además produce un arrastre parcial del mismo con una
velocidad va cuya magnitud está definida por la ecuación 4.5.2 que es:
Δρ
va=vm
ρa+Δρ
Δρ
o bien
va=vm α
donde
α=
(11.8.2)
ρa+ Δρ
El factor α es el coeficiente de arrastre del éter por la masa m.
De acuerdo con la ecuación 11.7.1 la velocidad de la luz en el interior de un cuerpo
transparente será:
c
Y
Y
Y
u=
donde
luego
y también
n
c=√ρa
u=√
ρ
u=√ρa n2
donde ρa es la densidad de nuestro éter ambiental y ρ será la densidad del éter en el
interior del cuerpo transparente.
Y
Y
Como
resulta
ρ=ρan2
√
ρ
=√ρa n2
pero
ρ=ρa+ Δρ
que nos lleva a
ρa+Δρ=ρan2
ρa
1
de donde obtenemos
=
n2
ρa+ Δρ
ρa+ Δρ-Δρ
1
Δρ
que convertimos en
=
=1-
n2
ρa+ Δρ
ρa+Δρ
Δρ
1
y finalmente en
=1-
ρa+ Δρ
n2
Δρ
1
Según la ecuación 11.8.2:
α=
luego
α=1-
ρa+ Δρ
n2
Con lo cual hemos llegado a la misma ecuación 11.8.1 que corresponde al coeficiente de
arrastre determinado experimentalmente.
Este resultado es una valiosa prueba para demostrar la existencia del éter, así como del
campo gravitónico que se produce en las pequeñas distancias que separan los átomos
que constituyen el material transparente.
11.9. Los diferentes fenómenos ópticos.
La luz produce una gran variedad de fenómenos, como son: la refracción, la reflexión, la
interferencia, la difracción, la dispersión, la polarización y algunos más.
Un estudio completo de estos fenómenos siguiendo los nuevos conceptos de la teoría del
éter, supondría una tarea de tal magnitud que hace imposible que el autor pueda
desarrollarla para ser incluida en el presente trabajo, por lo cual nos limitaremos a analizar
someramente la relación que existe entre estos fenómenos y el éter.
11.10. La refracción de la luz.
A lo largo del tiempo ha habido diferentes opiniones sobre la naturaleza de la luz y
podemos recordar que Newton proponía que la luz tenía naturaleza corpuscular. Esta idea
se mantuvo mucho tiempo hasta que se comprobó que la velocidad de la luz era menor
en los cuerpos transparentes que en el vacío, lo que estaba en contradicción con la teoría
de Newton, según la cual las partículas resultarían aceleradas al adentrarse en los
cuerpos transparentes. Por otro lado los experimentos de Young, al poner de manifiesto el
fenómeno de la interferencia, convencieron a los físicos de que la luz tenía naturaleza
ondulatoria. Pero de nuevo surgieron serias dudas cuando Einstein demostró el
comportamiento cuántico de la luz, que solo tiene explicación si ésta tiene naturaleza
corpuscular.
Seguidamente trataremos el fenómeno de la refracción y comprobaremos que se puede
explicar igualmente como un fenómeno ondulatorio, que como un fenómeno gravitatorio,
gracias a la existencia del éter en el cual se producen campos gravitónicos.
Se conoce como refracción de la luz la desviación que sufre un rayo luminoso al pasar de
un medio de propagación a otro medio con diferente velocidad de propagación.
El índice de refracción de un cuerpo transparente ha sido definido como la relación que
existe entre la velocidad de propagación de la luz en el vacío y la velocidad dentro del
cuerpo transparente:
c
n=
u
Está demostrado que el ángulo de incidencia α1 y el ángulo de refracción α2 referidos a la
normal a la superficie según la fig. 11.10.1 obedecen a la siguiente ecuación, conocida
como ley de Snell:
sen α1 n1=senα2 n2
(11.10.1)
α1
n1
n2
α2
fig. 11.10.1
Esta ley se demuestra aplicando el principio de Huygens, que considera el frente de onda
como la envolvente de pequeñas ondas esféricas.
α1
n1
n2
α2
fig. 11.10.2
En la figura 11.10.2 se demuestra que en el mismo tiempo que la luz recorre la distancia a
en el medio n1, recorre la distancia d en el medio n2 por lo cual:
a
d
a
d
sen α1=
; senα2=
luego
b=
=
b
b
senα1
sen α2
Δ tv1
Δ tv2
pero
a=Δtv1
y
d=Δtv2
luego
=
senα1
sen α2
de donde resulta:
sen α2 v1=senα1v2
c
c
c
c
pero
v1=
y
v2 =
luego
sen α2
1=senα1
n1
n2
n1
n2
y finalmente tenemos:
sen α2 n2=senα1 n1
Nota aclaratoria: Los ángulos de la fig. 11.10.1 referidos a la normal a la superficie tienen
el mismo valor que los ángulo de la fig. 11.10.2 referidos a la superficie, porque el frente
de onda es perpendicular a la trayectoria.
Para poder interpretar la refracción de la luz como un fenómeno gravitatorio, deberemos
considerar las siguientes circunstancias que concurren en el mismo:
ρ1 a n12
ρ2 a n22
fig. 11.10.3
Gradiente de ρ
La densidad ρ del éter es proporcional a n2. Debido a que la densidad del éter en el interior
de un cuerpo es mayor que en el exterior del mismo, sobre la superficie del mismo se
origina un gradiente de la densidad del éter, que a su vez da lugar a un campo
gravitónico, tal como se ha demostrado en el capítulo 4. El alcance de este campo es muy
pequeño y podríamos estimar que se hace despreciable a una distancia poco mayor que
la separación entre los núcleos atómicos.
Por último deberemos recordar que los fotones están asociados a una onda
electromagnética que se propaga con una velocidad que es función inversa de la
densidad del éter, de acuerdo con la ecuación 7.2.3.
En la fig. 11.10.4 se representan las fuerzas a que está sometida la masa de un fotón que
pasa de un medio a otro con mayor densidad del éter.
ρ1 a n12
Gradi
e
n
t
e
ρ2 a n22
V1
F
1
Fg
V2
V2
F
1
Fg
V1
F
r
V2
Fg
F
1
F
r
V1
fig. 11.10.4
La fuerza Ff es una fuerza de frenado con la misma dirección que la trayectoria, que se
produce al superarse la velocidad crítica de propagación.
La fuerza Fg es la fuerza gravitónica que produce el gradiente de la densidad del éter
sobre la masa del fotón. Esta fuerza tiene en todo momento una dirección perpendicular a
la superficie.
La fuerza Fr es la resultante de la suma vectorial de Ff y Fg.
Cuando el fotón incide con una trayectoria perpendicular a la superficie, la fuerza
resultante Fr tiene la misma dirección que la trayectoria, por lo cual ésta no sufre
desviación. Solo disminuye la velocidad.
De la figura 11.10.4 se deduce que la desviación sufrida por los fotones después de
atravesar la región con gradiente de densidad del éter, resulta mayor cuando el ángulo de
incidencia es mayor.
Si los fotones se desplazaran en sentido contrario al representado en la figura, la
trayectoria tenderá a separarse de la perpendicular, siguiendo el proceso inverso al
representado en la fig. 11.10.4.
Las fuerzas que intervienen en este fenómeno tienen una magnitud variable a lo largo del
recorrido en la zona de gradiente, puesto que dependen de la densidad del éter.
Debido a que no conocemos todavía la relación cuantitativa que existe entre los factores ρ
y K1 que intervienen en el proceso de refracción, no es posible hacer una demostración
matemática de que la trayectoria de los fotones se rige por la ley de Snell. Por otro lado la
dispersión de los colores parece demostrar que la velocidad de propagación no depende
exclusivamente de la densidad del éter interior, pues debido a la movilidad de las
partículas que constituyen el cuerpo transparente, se produce una vibración que origina
una reemisión de ondas que interfieren con las ondas incidentes, dando por resultado una
velocidad de propagación que depende de la frecuencia de la luz y de la estructura del
material.
No obstante, la explicación de la refracción de los fotones como un fenómeno gravitónico
o gravitatorio es compatible con la ley de Snell que solo considera las ondas, por lo cual
podemos asumir que esta ley rige la trayectoria de los fotones.
Como conclusión podemos afirmar que la velocidad de los fotones es la misma que la
velocidad de propagación de las ondas electromagnéticas, pero su trayectoria depende de
los campos gravitónicos o gravitatorios, mientras que es independiente de los campos
eléctricos o magnéticos.
La ineficacia de los campos eléctricos y magnéticos sobre los fotones se debe a que estos
están constituidos por pares de cargas de signo opuesto que resultan eléctricamente
neutros, puesto que cada uno de los electrinos sufrirá una fuerza con sentido contrario a
la otra.
11.11. La reflexión de la luz.
La teoría de las ondas electromagnéticas da una explicación plenamente satisfactoria del
fenómeno de la reflexión de la luz cuando ésta es considerada como una pura onda
electromagnética, pero no puede explicar el fenómeno si consideramos la naturaleza
corpuscular de la luz.
Una onda puede ser reflejada con una fracción de la intensidad de la onda incidente, pero
resulta imposible que una partícula pueda ser reflejada parcialmente si no se divide en
dos partes, y el efecto fotoeléctrico demuestra que los fotones se reflejan o se absorben
íntegramente.
El problema queda resuelto si consideramos que la intensidad de un rayo luminoso está
determinada por la cantidad de fotones que inciden en la unidad de superficie por unidad
de tiempo, en lugar de considerar la intensidad de la onda electromagnética, que deberá
ser la misma en cada fotón de la misma frecuencia.
Con este criterio, el coeficiente de reflexión es la relación entre el número de fotones
reflejados y el número de fotones incidentes:
Nr
β=
Ni
Pero ahora surge una pregunta: ¿por qué se reflejan en la superficie de un cuerpo solo
una parte del número total de fotones incidentes, mientras otra parte es absorbida o
propagada a través del mismo?
Sin entrar en un análisis riguroso, vamos a dar una explicación somera de este fenómeno,
basándonos en la existencia del campo gravitónico que se produce por el gradiente de
densidad del éter, según queda explicado en la sección 4.2.
En la fig. 11.11.1 se representa de forma esquemática el perfil de un cuerpo transparente
con la región superficial donde se produce un gradiente de densidad en el éter.
Sabemos ya que este gradiente da lugar a un campo de fuerza gravitónico, pero además
en las proximidades de los núcleos atómicos que constituyen el cuerpo, se originan
fuertes campos gravitónicos, que se representan por circunferencias concéntricas.
En la figura se representan tres fotones que inciden paralelamente sobre la superficie con
las trayectorias A, B y C.
A
B
g
ρ
C
fig. 10.11.1
Estos fotones sufren procesos diferentes que vamos a describir seguidamente:
En el caso A el fotón recorre una zona con gradiente, donde es refractado y después
sigue un recorrido rectilíneo al atravesar una región con densidad casi uniforme.
En el caso B la trayectoria se acerca a un átomo y es desviada por su campo gravitónico,
al mismo tiempo que disminuye su velocidad y aumenta su masa inercial. Las leyes de la
mecánica obligarán al fotón a seguir una trayectoria que lo devuelve hacia la superficie
con un ángulo de salida simétrico al de entrada, perdiendo masa inercial y recuperando la
velocidad inicial. Se ha producido un proceso de reflexión.
En el caso C el fotón hace impacto sobre un electrón y resulta absorbido por el mismo,
aumentando la masa y la energía de este.
Esta absorción puede ir seguida de una reemisión de fotones en cualquier dirección, lo
cual constituye un efecto que es conocido como dispersión de la luz.
Resulta evidente que la cantidad de fotones que serán reflejados, refractados o
absorbidos, dependerá de la estructura del material y también del ángulo de incidencia.
Existen sustancias que apenas reflejan la luz y además son opacas. En estas sustancias
la luz es absorbida y después se produce una radiación con diferente frecuencia,
generalmente una radiación térmica.
11.12. Interferencia de la luz.
Los fenómenos de interferencia y difracción tienen una explicación satisfactoria cuando se
considera que la luz es simplemente una onda electromagnética. Entonces estos
fenómenos son tratados como una simple interferencia de ondas, que la física ha
estudiado profusamente.
En la fig. 11.12.1 se representa en el caso típico de interferencia resultante entre las
ondas procedentes de las ranuras S1 y S2 que son coherentes porque reciben ambas una
parte de la misma onda que ha pasado por la ranura So.
P
S1
I
G
S0
S2
fig. 11.12.1
La curva I expresa la intensidad de la luz recibida en la pantalla P.
Sin embargo, cuando pasamos a considerar la naturaleza corpuscular de la luz, a lo cual
nos obliga la evidencia del efecto fotoeléctrico, esta interpretación no resulta válida.
Ya no podemos admitir que los fotones se dividen en dos partes para luego reunirse
dando lugar a una intensidad de la onda de acuerdo con el resultado de la interferencia.
Los fotones se mantienen completos y la intensidad de su campo electromagnético es
constante cuando se desplazan. Los fotones están en un lugar del espacio o no están allí,
ese es el dilema.
Sin pretender establecer una teoría completa sobre la interferencia de la luz, vamos a
exponer algunos criterios basados en la teoría del éter que permiten dar una explicación
razonada sobre las causas que originan los fenómenos de interferencia en las radiaciones
fotónicas.
Sabemos que la intensidad de un rayo de luz está determinada por la cantidad de fotones
que inciden en la unidad de tiempo sobre una unidad de superficie, por consiguiente
deberemos buscar como origen de las franjas de interferencia algo que provoca una
especial distribución de las trayectorias de los fotones, algo que obligue a esas
trayectorias a agruparse sobre ciertas franjas preferentes, como demuestra la experiencia.
En el capítulo 8 se demuestra que una carga eléctrica desplazándose a la velocidad de
propagación de las ondas no puede sufrir ninguna fuerza debida a campos eléctricos o
magnéticos, además los fotones tienen una carga eléctrica equilibrada que los hace
eléctricamente neutros.
También la experiencia ha demostrado que la luz no puede ser desviada por campos
eléctricos o magnéticos.
Sin embargo la luz resulta desviada por los campos gravitatorios, como se ha
comprobado en los rayos de luz que pasan cerca del sol o de algunas estrellas, o como
se ha demostrado en la sección 11.10 al tratar la refracción de los fotones.
Estas consideraciones nos inducen a pensar que no son los campos electromagnéticos
los causantes de la interferencia o la difracción de la luz, sino las campos gravitatorios o
gravitónicos, y que es la interferencia de las ondas gravitatorias lo que puede explicar los
fenómenos de interferencia de la luz o de cualquier radiación fotónica.
Pero ahora nos preguntamos: ¿cómo se producen las ondas gravitatorias? ¿por qué estas
ondas gravitatorias tienen la misma longitud de onda que los fotones? ¿por qué se
producen las ondas gravitatorias cando un rayo de luz pasa muy cerca del borde de un
obstáculo o a través de unas rendijas? ¿cuál es la naturaleza de las ondas gravitatorias?
Basándonos en la teoría del éter podremos dar una respuesta a todas estas preguntas, lo
cual haremos empezando por la última pregunta.
En el capítulo 2 se explica que el éter no penetra en el interior de las partículas
subatómicas, las cuales son consideradas de materia compacta.
Por esta razón, cuando estas partículas se desplazan con un movimiento acelerado se
produce una onda de presión en el éter, que lleva implícito un incremento de la densidad.
Este fenómeno constituye lo que se conoce como ondas gravitatorias.
Las ondas gravitatorias se rigen por las mismas leyes que la física clásica ha establecido
para tratar el movimiento ondulatorio en un fluido elástico, como es el caso de las ondas
acústicas, pero exceptuando la influencia de la temperatura que afecta a los gases.
La mecánica clásica demuestra, según se explica en la sección 7.2 que la velocidad de
propagación de una onda longitudinal depende de la densidad del medio y del módulo de
compresibilidad B, según la ecuación 7.2.2:
B
vp=√ρ
t5
t
4
t3
t2
t1
-
-
-
-
-
u
+E
+
-
-E
λ
2
fig. 11.12.2
En la fig. 11.12.2. se representa el movimiento que realiza un electrón anular bajo el
efecto del campo eléctrico asociado a un fotón que se desplaza a corta distancia del
mismo.
El desplazamiento del electrón respecto al centro de gravedad del átomo varía su sentido
desde el instante t1 hasta el instante t5, realizando un movimiento de rotación.
La oscilación del electrón respecto al centro de gravedad del átomo, generará una onda
gravitatoria con la misma longitud de onda que el fotón que la ha provocado, tal como se
representa en la figura.
La intensidad de la onda gravitatoria será función de la aceleración del electrón y de la
superficie del mismo. La aceleración dependerá de la intensidad del campo eléctrico
procedente del fotón y por lo tanto de la distancia que los separe, de acuerdo con la
ecuación 11.5.5.
El núcleo de los átomos con carga positiva también resultará sometido a una oscilación
cuando un fotón pasa cerca, generando una onda gravitatoria con fase opuesta a la
producida por los electrones, debido a que su carga eléctrica es de signo contrario. Esta
onda podría anular la onda emitida por los electrones si tuviera la misma magnitud, pero
los núcleos tienen una masa que es como mínimo 1800 veces mayor que la masa de los
electrones, mientras que su superficie no supera la de éstos, por lo cual su aceleración
será reducida en la misma proporción y consecuentemente la intensidad de la onda
gravitatoria resultará muy pequeña respecto a la provocada por los electrones.
Una vez explicada la naturaleza de las ondas gravitatorias y la posibilidad de ser
provocadas por la proximidad de los fotones, deberemos encontrar la causa que obliga a
los mismos a comportarse como si estuvieran sometidos a un proceso de interferencia de
ondas, sabiendo que son corpúsculos.
Para facilitar la explicación dividiremos el proceso en dos etapas: en primer lugar
analizaremos lo que sucede con los fotones cuyas trayectorias pasan por las
proximidades de un obstáculo y después consideraremos el efecto de la interferencia de
las ondas gravitatorias sobre los fotones.
A causa del campo gravitónico que se produce en las cercanías de las partículas de
masa, cuando un fotón pasa cerca de la superficie de un obstáculo, sufrirá una fuerza que
desviará su trayectoria. En la fig. 11.12.3 se representan las trayectorias de varios fotones
que antes de desviarse eran paralelas entre sí.
fig. 11.12.3
En la fig. 11.12.4 se representan las trayectorias de los fotones que atraviesan una ranura
estrecha, provocando una dispersión en forma de abanico, debido a que la desviación es
mayor cuando la distancia al obstáculo es más pequeña.
fig. 11.12.4
Ahora deberemos explicar lo que sucede con los fotones que avanzan por un campo en el
cual se produce la interferencia de dos ondas gravitatorias coherentes entre sí:
En la fig. 11.12.5 se representa un fotón que pasa por la ranura So donde sufre una
desviación al mismo tiempo que provoca una onda gravitatoria de su misma frecuencia.
Esta onda gravitatoria alcanza las ranuras S1 y S2 en los cuales se originan sendos focos
que radian dos ondas coherentes.
P
I
S1
S0
S2
fig. 11.12.5
La interferencia de estas ondas creará en el éter puntos de máxima densidad en aquellos
lugares en los que las dos ondas coinciden en su fase de máxima intensidad. En la figura
se puede observar que estos puntos quedan ordenados formando unas franjas que
contienen un incremento de la densidad del éter y consecuentemente un gradiente de
densidad capaz de producir una fuerza sobre las partículas de masa que constituyen los
fotones.
Cuando un fotón pase a través de una de las ranuras S1 o S2 resultará desviado hacia las
franjas de mayor densidad del éter y su trayectoria tenderá a seguir el camino marcado
por las mismas hasta incidir sobre la pantalla P.
Cuando el número de fotones es muy elevado, sobre la pantalla se producirán unas
bandas luminosas cuya intensidad dependerá de la cantidad de fotones que incidan en la
unidad de tiempo sobre la unidad de superficie. Esta intensidad será proporcional a la
intensidad que tendría en los mismos puntos el resultado de la interferencia de dos ondas
de cualquier naturaleza con la misma longitud de onda.
El comportamiento de los fotones en un campo de interferencia de ondas gravitatorias
permite tratar los fenómenos de interferencia de la luz como si ésta estuviera constituida
por ondas electromagnéticas, a pesar de que su naturaleza es distinta.
El modo de tratar la interferencia de la luz como una interferencia de ondas
electromagnéticas ha sido ampliamente desarrollado por la física clásica, por lo cual
resulta innecesario repetir aquí las explicaciones de los diferentes casos que se producen
en la práctica.
11.13. Polarización de la luz.
Es un hecho demostrado experimentalmente que la luz se comporta en algunos casos
como una onda electromagnética que tiene un campo electromagnético con sentido
perpendicular a la dirección de propagación, dando lugar a una serie de fenómenos que
han sido estudiados detalladamente por algunos científicos.
En la sección 11.5. se ha hecho una descripción básica de los fotones en la cual queda
incluida la polarización eléctrica de los mismos, que es perfectamente compatible con los
fenómenos observados, por lo cual resulta superfluo repetir ahora la explicación de estos
casos que ya son conocidos.
11.14. Aberración de la luz estelar.
Se conoce como aberración de la luz estelar un efecto de desviación de la luz procedente
de las estrellas, que fue detectado por el astrónomo británico Bradley en el año 1725,
quien observó que la posición aparente de una estrella sufría una desviación que
resultaba de valor máximo cuando se comparaban entre sí las posiciones observadas
desde dos puntos opuestos diametralmente sobre la órbita terrestre alrededor del sol. En
el transcurso de un año la posición aparente de una estrella describía una elipse en cuyo
centro debía estar la posición real.
En la fig. 11.14.1 se representan cuatro posiciones aparentes que se observan desde
cuatro puntos correlativos de la eclíptica, en los cuales se indica con un vector la
velocidad de la tierra.
Posiciones aparentes
1
2
Posición real
4
3
90º
2
3
Sol
fig. 11.14.1
1
4
Tierra
Este fenómeno se interpretó correctamente como la consecuencia del movimiento de la
tierra en su órbita solar, de modo que la orientación del telescopio quedaba determinada
por la velocidad de la luz (c) y la velocidad de traslación del telescopio (v) transportado por
la tierra, según se representa en la fig. 11.14.2.
El ángulo de desviación α queda determinado por las relaciones siguientes:
b
v
sen α=
donde
b=v senθ luego
sen α=
senθ
c
c
v
α
θ
v
α
fig. 11.14.2
θ
θ
La diferencia entre dos posiciones diametralmente opuestas resulta β=2α y alcanzará su
máximo valor entre las posiciones 2 y 4 de la fig. 11.14.1, en las cuales el ángulo θ entre
v
el vector v y la trayectoria de la luz es de 90º con senθ=1, por lo cual
sen α=
, que es la
c
máxima desviación posible.
Como la velocidad de la luz se estima en 3x108 m/s y la tierra se desplaza en su órbita
solar a una velocidad de 3x104 m/s se puede calcular el valor de la desviación que se
produce:
4
v
3x10
sen α=
senθ; senα=
senθ; sen α=10-4 senθ
c
3x108
Los resultados obtenidos por las observaciones realizadas por Bradley sobre la estrella
Gamma Dragon correspondían con gran aproximación a este valor.
Las conclusiones que se deducían de estos experimentos eran que la luz podía tener
naturaleza corpuscular y seguir una trayectoria inercial, o por el contrario tenía naturaleza
ondulatoria y se propagaba por medio de un éter fijo en el espacio a través del cual se
desplazaba la tierra.
Sin embargo no podía aceptarse un éter que acompañase a la tierra en su movimiento, si
al mismo tiempo se consideraba la naturaleza ondulatoria de la luz.
11.15. El experimento de Michelson.
En la época en que se realizó este experimento, efectuado por primera vez en 1881, se
tenía el convencimiento de que la luz era un fenómeno ondulatorio que se producía en el
éter y que este permanecía fijo en el espacio, de modo que la tierra se desplazaba a
través del mismo.
Michelson tuvo conocimiento, ocasionalmente, de que Maxwell había concebido la
posibilidad de calcular el desplazamiento del sistema solar respecto al éter fijo, lo que le
indujo a meditar sobre el asunto y en un alarde de ingenio inventó un procedimiento
basado en la interferencia de un rayo de luz propagándose en la dirección del movimiento
de la tierra con otro rayo de la misma luz que tenía un recorrido perpendicular al anterior,
consiguiéndose una precisión extraordinaria.
No se describen aquí los detalles de este experimento por considerar que ha sido
suficientemente divulgado en muchos tratados de física.
El resultado del experimento fue decepcionante, pues a pesar de su gran precisión no
acusó ningún movimiento relativo entre la tierra y el éter fijo. Posteriormente se han
realizado numerosos experimentos, cada vez más precisos, pero nunca se ha obtenido
algún resultado que demuestre la existencia de un éter fijo en el espacio.
Por otro lado, si se consideraba un éter arrastrado por la tierra no se podía explicar el
efecto de la aberración de la luz de las estrellas según las leyes correspondientes a una
propagación ondulatoria. Solamente era compatible con una luz compuesta por partículas
que se propagan inercialmente, pero esta última opción era incompatible con los
fenómenos de interferencia.
La confusión que se originó fue muy grande y tuvo como consecuencia el rechazo del éter
como medio de propagación de las ondas electromagnéticas. Maxwell propuso la
propagación en el vacío, lo cual fue después reafirmado por Einstein con su teoría de la
Relatividad Especial que prevalece hasta nuestros días.
En esta teoría del éter se demuestra que no hay contradicción entre la aberración de la
luz estelar y el resultado nulo del experimento de Michelson, por las siguientes razones:
1ª.- Los fotones están constituidos por partículas con masa, por lo cual siguen una
trayectoria inercial.
2ª.- El éter acompaña a la tierra porque está sujeto a las leyes gravitatorias y por
consiguiente está obligado como cualquier planeta a orbitar alrededor del sol. Es parte del
sistema.
3ª.- Los fotones están asociados con una onda electromagnética que los acompaña, lo
cual provoca los fenómenos de interferencia como se demuestra en la sección 11.12.
aunque la luz no es una mera onda electromagnética.
11.16. Lentes gravitatorias.
Al estudiar el campo gravitatorio en el capítulo 3 vimos que alrededor de una masa se
produce un incremento en la densidad del éter, de modo que la densidad absoluta
resultante, según la ecuación 3.2.2 será:
k2m
ρ=ρa+
r
Como los astros están constituidos por grandes masas, una consecuencia inmediata es
que en su entorno se creará un gradiente en la densidad del éter, que a su vez constituye
un campo gravitatorio.
Este gradiente de densidad provoca la refracción de la luz, lo mismo si consideramos el
fenómeno bajo el criterio de las ondas, que si lo consideramos como un efecto
gravitatorio, como hemos explicado en la sección 11.10.
No es necesario recurrir a la Teoría de la Relatividad General con sus oscuros principios,
para explicar este fenómeno que es simplemente un proceso de refracción como el que
se produce en la atmósfera por el gradiente de densidad. Este fenómeno de refracción ha
sido comprobado en las proximidades del sol, aprovechando un eclipse y observando la
luz procedente de una estrella.
fig. 11.16.1
El experimento ha sido realizado varias veces con la idea de confirmar las predicciones de
la relatividad General y el resultado ha dado unos valores comprendidos entre 1,6 y 1,98
segundos de arco.
Anteriormente, en el año 1801, el astrónomo alemán Soldner había calculado la
trayectoria de un rayo de luz en las proximidades del sol, tratándola simplemente como
partículas con masa y aplicando las leyes de Newton. Sus cálculos daban como resultado
una desviación de 0,875 segundos de arco. Los cálculos de Einstein predicen una
desviación de 1,75 segundos.
La teoría del éter no puede ofrecer todavía un valor numérico para esta desviación porque
en la actualidad no conocemos el valor numérico de la constante k2 ni de la densidad
básica del éter ambiental ρa de la ecuación 3.2.2, pero podemos asumir que debería ser
algo mayor que la calculada por Soldner, porque en sus cálculos no consideró que existe
lo que se conoce por “viento solar”, el cual deberá influir en la refracción aumentando la
desviación. Einstein tampoco tuvo en cuenta este factor, que actualmente resulta
imponderable y además no es de magnitud constante, pues se sabe que en el sol se
producen emisiones irregulares de partículas.
Después de estas consideraciones deberemos pensar que no es el valor numérico más
aproximado el que nos lleva más cerca de la verdad, puesto que a la imprecisión de la
medida se suma la emisión del viento solar que es variable en el tiempo. La dispersión de
los resultados experimentales obtenidos hasta ahora puede ser causada por el viento
solar.
a
b
fig. 11.16.2
Debido a que la densidad del éter alrededor de un astro es función de m/r la lente
gravitatoria que se produce no equivale a una lente esférica cuyo material tiene una
densidad uniforme. Su equivalente en un vidrio de densidad uniforme deberá tener un
perfil semejante al representado en la fig. 11.16.2 b que produce el mismo efecto de
refracción que un campo gravitatorio que se ha representado en a.
Es fácil construir una lente de plástico de este tipo y
A'
comprobar sus efectos, pues produce imágenes muy
A
distorsionadas si las comparamos con las lentes esféricas
que utilizamos habitualmente.
Una pequeña fuente de luz de forma circular (A) situada
en el eje óptico de la lente producirá para el observador
situado en (B) una imagen en forma de anillo (A’) tal como
muestra la fig. 11.16.3.
B
fig. 11.16.3
A'
A'
A
Si la fuente se desvía cierto ángulo respecto al eje, la
imagen que ve el observador desde el punto B se
convierte en dos segmentos de arco desiguales,
como ilustra la fig. 11.16.4.
B
fig. 11.16.4
En el caso de que la fuente de luz (A) esté
A'
A
suficientemente desviada del eje óptico, el observador
podrá ver simultáneamente la imagen real y además otra
imagen virtual situada en A’ según la fig. 11.6.5.
B
fig. 11.16.5
Todos estos fenómenos son observados en los últimos tiempos por los astrónomos y son
considerados como una confirmación de la Relatividad General, pero ya hemos
demostrado que tienen una explicación más sencilla basada en la refracción que provoca
el éter al incrementar su densidad en las proximidades de los astros.
12.1. ¿Qué es la energía?
La energía ha sido definida como la capacidad de un sistema para producir un trabajo.
Pero deberemos asumir que la energía no es un ente que existe por si mismo, sino que es
un estado de la masa, como es la velocidad o la cantidad de movimiento. La energía no
tiene significado alguno sin la presencia de una masa, ya que es un atributo de la misma.
Cuando la energía se manifiesta explícitamente como una masa en movimiento se la
denomina “energía cinética” y su magnitud está definida por la siguiente ecuación:
1
E=
Mv2
(M = masa inercial)
2
Esta ecuación define la naturaleza esencial de la energía. Se denomina “energía
potencial” la capacidad latente de un sistema para producir un trabajo en un momento
determinado bajo ciertas condiciones.
Cualquier forma de energía, como la energía térmica, la electromagnética, la química, la
luminosa, etc, es esencialmente energía cinética, aunque en algunas ocasiones está
sustentada por la masa del éter, como se ha demostrado en las secciones 6.8, 7.8 y 11.3.
En el vacío absoluto no se puede almacenar energía alguna, puesto que el vacío no tiene
ninguna propiedad física. Es el éter el que proporciona la capacidad de almacenar energía
potencial en los campos de fuerza gravitatorios, eléctricos, etc.
La energía no puede ser considerada una magnitud absoluta, como es el criterio de
algunos científicos, pues debido a que cualquier forma de energía es esencialmente
energía cinética y ésta depende de la velocidad de la masa, finalmente resulta que la
energía es una magnitud relativa por serlo la velocidad.
La energía pierde todo significado cuando no existe un sistema de referencia, como
demostraremos a continuación.
Imaginemos dos masas moviéndose en el espacio con sus velocidades respectivas según
se representan en la fig. 12.1.1 Las velocidades v1 y v2 están referidas en este caso a un
marco de referencia que se considera fijo.
V1
V2
m1
m2
fig. 12.1.1
Si eliminamos el marco de referencia y dejamos las dos masas en un universo
absolutamente vacío, según la figura 12.1.2 solo tendrá significado el movimiento relativo
entre las dos masas.
V = 0
1
V
fig. 12.1.2
m
1
m2
Podemos considerar que una de las dos masas está en reposo y la otra se mueve
respecto a la primera, o viceversa.
Finalmente eliminamos una de las dos masas, dejando una masa única en un universo
vacío, según la fig. 12.1.3.
?
fig. 12.1.3
m1
Ahora ya no tendrá significado la velocidad, ni la energía, ni la cantidad de movimiento de
esta masa, quedando demostrado que estas magnitudes tienen carácter relativo y solo
pueden ser definidas con relación a un sistema de referencia determinado.
Ahora sabemos que todos los campos de fuerza existentes, ya sean gravitatorios,
eléctricos o magnéticos tienen su soporte real en el éter. Por consiguiente, si
consideramos el éter como el marco de referencia del movimiento y de la energía,
habremos conseguido establecer un sistema en el cual todos los fenómenos resultan
coherentes.
Cuando en dos regiones del espacio el éter tenga un movimiento relativo, deberemos
considerar esta circunstancia para poder aplicar las leyes físicas sin cometer error. Este
es el caso de la aberración de la luz estelar.
12.2. La masa no es equivalente a la energía.
La Teoría de la Relatividad Especial postula que la masa puede convertirse en energía y
viceversa, de modo que establece entre ella una equivalencia que es:
E=mc2
En la teoría del éter se rechaza este postulado y se afirma que la masa gravitatoria es una
magnitud absoluta y constante, mientras la energía es una magnitud relativa debida al
movimiento de la masa inercial y además esta última depende de la densidad del éter.
Podríamos decir que la masa es portadora de la energía. En el caso concreto de las
radiaciones fotónicas hemos demostrado que la masa de los fotones transporta una
cantidad de energía cinética y otra cantidad de igual magnitud de energía
electromagnética, de modo que la energía total de un fotón es:
E = 2(12 Mc2) E = Mc2y generalizando E = Mu2
En la última ecuación empleamos el símbolo (u) para expresar la velocidad de
propagación, debido a que ya hemos demostrado que las ondas luminosas no tienen una
velocidad constante como significa la letra c, sino que la velocidad de propagación u
depende de la densidad del éter.
Hasta ahora ha sido utilizado el criterio de la conversión de la masa en energía, o la
equivalencia masa-energía para explicar los procesos de desintegración nuclear y la
reacción entre partículas, consiguiéndose un buen acuerdo entre los resultados
calculados y los resultados experimentales, lo que nos obliga a preguntar: ¿es posible
explicar estos mismos procesos bajo el principio de la conservación de la masa sin
aceptar su transformación en energía?
La respuesta es afirmativa y se demostrará en la sección siguiente.
12.3. Transformación de partículas.
Bajo este epígrafe consideraremos cualquier clase de transformación, ya sea la reacción
entre partículas subatómicas, o la desintegración de los núcleos atómicos.
Cualquier proceso de transformación puede ser explicado considerando los siguientes
principios:
1.- Conservación de la masa gravitatoria total (m).
2.- Conservación de la carga eléctrica neta.
3.- Conservación de la energía total, incluyendo la energía potencial.
4.- Conservación de la cantidad de movimiento (suma vectorial de Mv).
Además se deberá tener en cuenta que la energía del fotón es Mu2, donde M es la masa
inercial y u es la velocidad de propagación que depende de la densidad del éter (ver
secciones 7.2. y 9.2.).
Seguidamente vamos a aplicar estos principios al caso típico de la reacción entre un
electrón y un positrón, en el cual se destruyen ambas partículas y se generan dos fotones
gamma.
En este caso se considera que la velocidad inicial de las partículas es nula o despreciable
al tomar contacto.
q1
q2
E= M3u2
E= M4u2
m1
m2
m3
m4
fig. 12.3.1
Antes del contacto
Después de la reacción
Tendremos:
1) m1 + m2 = m3 + m4
2) q1 + q2 = 0
3)
EE1+EE2=M3u2 + M4u2
Donde EE1 es la energía potencial del campo eléctrico.
La masa de los fotones m3+m4 es igual a la masa del positrón más la masa del electrón
m1+m2.
La suma de las cargas eléctricas, por ser iguales y de signo contrario se anulan
mutuamente, lo que está de acuerdo con la ausencia de carga neta en los fotones
resultantes.
La energía
EE1+EE2
correspondiente a las cargas del positrón y del electrón es igual a la
energía total de los dos fotones: M3u2+M4u2.
Finalmente, como los dos fotones marchan en sentidos opuestos con la misma velocidad
u y sus masas inerciales son iguales, resultará que la cantidad de movimiento del sistema
será nula, tal como era antes de la reacción.
Este caso se ha utilizado en alguna ocasión como “una clara evidencia de la conversión
de la masa en energía” pero queda demostrado que el mismo se explica perfectamente
aplicando los principios de conservación enumerados anteriormente y considerando el
nuevo concepto del fotón.
Resolvamos ahora el caso de una partícula neutra de masa m1 y con velocidad v1 que
reacciona con otra partícula que está en reposo, la cual tiene una masa m2 y una carga
eléctrica +q2, resultando de esta reacción dos partículas y un fotón.
Aplicando los cuatro principios de conservación tendremos:
m1
m2
m4
N
V1
m3
q4
q3
M5u2
q2
m5
fig. 12.3.2
Antes
Después
1) m1+m2 = m3+m4+m5
2) q2=q3+q4
1
1
1
3)
M1 v2+EE2 =
M3 v2+
Mv2+M5u2+ EE3+EE4
2
2
2
4)
M1 v1=M3 v3+M4
v4+M5v5
(suma vectorial)
Del mismo modo se pueden interpretar los procesos de desintegración de un núcleo que
se divide en varias partículas o el caso inverso en el cual se reúnen varias partículas para
constituir un núcleo.
En el año 1931 Pauli sugirió que sería necesario considerar la existencia de una partícula
a la cual se denominó neutrino, para poder justificar los resultados de determinados
procesos de transmutación.
Este neutrino no debería tener carga eléctrica y su masa tendría que ser nula o
extremadamente pequeña. Hasta el año 1953 no se pudo tener evidencia directa de la
existencia del neutrino. Actualmente se estima que su masa en reposo deberá ser nula o
menor que 0,05 veces la masa de un electrón.
De acuerdo con los principios de la teoría del éter, la masa es una magnitud constante y
por consiguiente la masa de los neutrinos en reposo no puede ser nula y deberá tener el
mismo valor que en estado de movimiento, aunque éste sea muy pequeño.
Es posible que en los procesos de transformación de partículas intervengan factores que
no se han considerado hasta ahora, como la radiación de ondas electromagnéticas puras
sin emisión de masa y con un espectro de frecuencias continuo, por lo que serían muy
difíciles de detectar. En el caso de suceder esto, la estimación de la energía total podría
resultar ligeramente afectada.
12.4. La energía nuclear.
En esta teoría del éter se postula la constancia de la masa gravitatoria y se rechaza la
conversión de la masa en energía, por lo cual surge una pregunta: ¿si la masa no se
convierte en energía, cual es el origen de la energía nuclear?
La explicación no es difícil si nos apoyamos en el principio de la conservación de la
energía, que dice que la energía total se conserva, incluyendo la energía potencial.
La energía nuclear proviene de la energía potencial debida a la carga eléctrica de los
protones que integran los núcleos, más la energía cinética almacenada en el movimiento
de rotación de los mismos:
ET =EE +EK
Tomando el valor de la energía del campo eléctrico cuando la carga está en reposo, no
será necesario considerar la energía del campo magnético, porque según se ha
demostrado en la sección 8.2. la suma de la energía del campo eléctrico más la energía
del campo magnético es una cantidad constante igual a la energía del campo eléctrico de
la carga en reposo.
Al fraccionarse un núcleo, la fuerza coeléctrica que retenía unidos entre si los protones y
los neutrones, ya no tiene efecto porque esta fuerza solo se produce en el contacto
directo y por consiguiente las partículas con carga eléctrica que han sido separadas entre
sí sufren la fuerza de repulsión originada por la presencia del éter, tal como se demuestra
en las secciones 5.2. y 5.3.
Al mismo tiempo, el fraccionamiento del núcleo con movimiento de rotación convierte una
parte de este movimiento en movimiento de traslación, liberando una parte de la energía
cinética almacenada en el movimiento de rotación.
Como producto de la desintegración de un núcleo atómico pueden surgir otros núcleos
más pequeños, además de neutrones, partículas intermedias, neutrinos, fotones y
radiaciones electromagnéticas puras, que deberán cumplir los cuatro principios de
conservación de la masa, de la carga, de la energía y de la cantidad de movimiento.
v
v
v
N
fig. 12.3.3
v
La energía que se produce en los procesos de fusión nuclear se explica siguiendo los
mismos criterios. La única diferencia es que en este caso el nuevo núcleo que se produce
tiene menor masa y energía potencial que la suma de los núcleos originales y
consecuentemente el exceso de masa y energía se convierte en radiación de fotones,
radiación de ondas electromagnéticas y emisión de algunas partículas que difieren en
cada caso.
13.1. El éter acompaña a los planetas.
El famoso experimento de Michelson y todos los que le siguieron después, cada vez con
más precisión, no pudieron detectar el movimiento de la tierra a través del éter fijo en el
espacio, por la sencilla razón de que el éter no permanece en reposo, sino que acompaña
a los planetas en su movimiento alrededor del sol, siguiendo las mismas leyes
gravitatorias, tal como hacen todos los elementos que constituyen el sistema solar.
El éter tiene masa y por consiguiente se moverá alrededor del sol con la misma velocidad
que los planetas situados a la misma distancia del sol. La fuerza gravitatoria deberá
equilibrar a la fuerza centrífuga.
La mayoría de los elementos que constituyen el sistema solar aparentan conservar una
cantidad del movimiento que compartían originariamente.
Tierra
Venus
Mercurio
Sol
fig. 13.1.1
De lo anterior se deduce que si queremos detectar la presencia del éter, será necesario
que el dispositivo detector se mueva con relación a la Tierra, dado que el éter está inmóvil
con relación a nuestro planeta.
En el caso de utilizar interferómetros como el de Michelson u otros similares, podría
obtenerse la detección del éter situando el dispositivo a bordo de un satélite artificial, pero
esta solución nunca ha estado al alcance del autor.
13.2. Dispositivo para detectar el éter.
Ante las dificultades para conseguir un experimento realizado a bordo de un satélite
artificial, el autor se esforzó en encontrar algún procedimiento que pudiera demostrar la
existencia del éter sin tener que desplazar el dispositivo a gran velocidad respecto a
nuestro planeta.
Después de dos años de búsqueda, el autor consiguió en el año 1993 desarrollar un
procedimiento que podría detectar la presencia del éter moviendo el dispositivo a una
velocidad tan baja como 1 mm por segundo.
El dispositivo se basa en la utilización de un láser He-Ne montado según se representa en
la fig. 13.2.1.
fig. 13.2.1
La disposición de los espejos formando un triángulo permite que la luz recorra un circuito
cerrado sin invertir nunca su sentido. El circuito será recorrido por la luz en ambas
direcciones y la frecuencia será la misma para ambos rayos de luz cuando el sistema se
encuentre en reposo respecto al éter.
La frecuencia de un láser queda determinada fundamentalmente por la frecuencia de
radiación propia de los átomos del gas utilizado, pero la frecuencia exacta queda
determinada por la siguiente ecuación:
Nc
fo=
l
donde N es número entero que corresponde al número de ondas completas que queda
comprendido en la longitud l, que es el recorrido que hace la luz para pasar dos veces por
el mismo punto, o dicho de otro modo l es la longitud del circuito.
En el caso de que no exista el éter, podremos girar el sistema alrededor de su centro
geométrico sin que la frecuencia del láser resulte alterada, de acuerdo con la teoría de la
Relatividad Especial, pero si el espacio está ocupado por el éter se deberá producir una
alteración en las frecuencias de ambos rayos de luz, puesto que el camino óptico
resultará aumentado para el rayo de luz que tiene el mismo sentido que la rotación del
dispositivo y quedará disminuido para el rayo que tiene sentido opuesto a dicha rotación.
Podemos determinar las dos frecuencias que resultarán cuando el sistema gire con una
velocidad tangencial v según se representa en la fig. 13.2.2.
v
fig. 13.2.2
Denominaremos
a la longitud del camino óptico que tiene el mismo sentido que la
rotación del aparato y
al camino con sentido opuesto a la rotación.
A la longitud del circuito la designaremos con
Nc
lc
lc
Tendremos:
ℓ1=
; ℓ2=
; fo=
c-v
c+v
ℓ
Nc
Nc(c-v )
Nc-Nv
Nc
Nv
Nc
f1 =
=
=
=
-
=
(1-vc )=fo(1-vc )
ℓ1
ℓc
ℓ
ℓ
ℓ
ℓ
Nc
Nc(c+v )
Nc+Nv
Nc
Nv
Nc
f2=
=
=
=
+
=
(1+vc )=f o(1+vc )
ℓ2
ℓc
ℓ
ℓ
ℓ
ℓ
Estas dos frecuencias pueden detectarse con un fotodiodo y así obtener otra frecuencia
que será la diferencia entre f1 y f2.
2v
Δf =f2-f1=fo(1+vc )-fo(1-v )=f oc
c
2fov
Δf =
(13.2.1)
c
Para detectar la diferencia de frecuencias entre los dos rayos de luz es necesario obtener
una muestra de cada rayo de luz y superponerlos adecuadamente para que incidan juntos
sobre un fotodetector, que nos proporcionará una onda eléctrica con una frecuencia que
será la diferencia entre las frecuencias de los dos rayos.
En la fig. 13.2.3 se representa el montaje del dispositivo sobre una plataforma giratoria.
E2
E3
E1
∆f
D
Fotodiodo
fig. 13.2.3
Motor
El espejo E3 tiene cierto grado de transparencia que permite que una fracción de la luz lo
atraviese para ser conducida al fotodetector D.
Utilizando un láser de helio-neón de 632,8 nm y aplicando una velocidad tangencial de 1
mm/s obtendremos los siguientes resultados:
c
3x108
f
=4,74 x1014c/s
v=10-3 m/s
o
=λ=632,8x 10-9
v
2fo
2x4,74x1014x10-3
Δf =
=
=3.160 c/s
c
3x108
Esta frecuencia de 3.160 c/s es audible mediante el uso de un altavoz y puede ser
observada en un oscilógrafo.
El láser deberá emitir luz polarizada linealmente para obtener un batido estable, además
uno de los espejos deberá ser ligeramente cóncavo para hacer posible el alineamiento de
los tres espejos entre sí.
Cuando el autor inició las gestiones para construir este dispositivo, fue advertido de que
un aparato similar ya había sido inventado para funcionar como giróscopo.
Efectivamente era similar al que había diseñado el autor para detectar el éter, había sido
realizado por J. Killpatrick y publicado en IEE Spectrum, Oct. 1967, p. 44.
Ya no hubo necesidad de construir este aparato, puesto que ya había sido realizado y
funcionaba como giróscopo, con lo cual quedaba demostrada la existencia del éter.
Pero la sorpresa del autor fue muy grande al comprobar que la explicación que se daba
sobre el funcionamiento de dicho “laser gyro” se basaba en la Relatividad General, sin
considerar la existencia del éter.
Es la explicación de su funcionamiento se dice que el cambio de longitud ΔL es dado por
4AΩ/c de acuerdo con la teoría de la relatividad general. Donde A es el área rodeada por
el camino de la luz, Ω es la velocidad angular y c es la velocidad de la luz. Expresando
esta fórmula en la misma terminología de este trabajo deberemos escribir:
Δℓ=4 Aw/c
(13.2.2)
El autor no conoce como se ha llegado a esta ecuación, pero se puede demostrar que es
equivalente a la demostración que hemos hecho para llegar a la ecuación 13.3.1 que se
basa en la existencia del éter, como comprobaremos seguidamente.
Para demostrar esta equivalencia bastará con expresar la diferencia de caminos ópticos
en función del área del triangulo constituido por el recorrido completo según se
muestra en la fig. 13.2.4.
a
b
fig. 13.2.4
c
lc ℓc 2ℓcv
Δℓ=ℓ
-ℓ2=
-
=
1
c-v
c+v
c2-v2
Pero v2 resulta despreciable en relación con c2, por lo cual tendremos:
2ℓcv
2ℓv
Δℓ=
=
c
c2
2 ℓrw
como v=wr resulta
Δℓ=
(13.2.3)
c
En el triangulo de la fig. 13.2.4 tenemos
=a+b+ c
1
1
y el área del triangulo es
A=
r (a+b+c)=
rℓ
2
2
por lo cual
rℓ=2 A
4 Δw
que llevado a la ecuación 13.2.3 la convierte en:
Δℓ=
c
que es la ecuación que ha sido empelada para explicar el funcionamiento del “laser gyro”.
14.1. Una teoría unificada.
Las demostraciones hechas a lo largo de este trabajo para explicar el campo gravitatorio,
el campo eléctrico y el campo magnético, confirman que en todos los casos en que se
produce una fuerza a distancia, la causa es siempre un desequilibrio en las fuerzas de
contacto directo con el éter, que ha sido alterado de modo diferente en cada caso.
Por consiguiente podemos afirmar que todos los fenómenos físicos en los que se
manifiestan fuerzas a distancia, tienen un origen común que es la fuerza coeléctrica que
se produce en el contacto directo con el éter, con lo cual queda establecida una teoría
unificada de los campos de fuerza.
El rechazo producido durante un siglo contra la idea de un éter real, había impedido
encontrar este origen común subyacente en los diferentes campos de fuerza, a pesar de
haberse perseguido con el máximo interés por algunos científicos.
Los motivos de que el éter haya sido rechazado son diversos: En primer lugar los modelos
de éter que habían sido propuestos, además de ser complicados, no satisfacían
plenamente las leyes físicas conocidas. Por otro lado el concepto puramente ondulatorio
que se tenía de la luz creaba dificultades para admitir la existencia del éter. Finalmente la
Relatividad Especial con sus postulados falsos bloqueaba definitivamente el
reconocimiento del éter.
Existe un buen acuerdo entre la Física del Eter y la Física Clásica después de hacer en
esta última algunas modificaciones que han sido expuestas y que no suponen un rechazo,
sino un perfeccionamiento de las mismas.
A lo largo de la exposición de esta teoría se han presentado de forma explícita en unos
casos y de forma implícita en otras ocasiones, una serie de principios que constituyen el
soporte de esta teoría del éter.
A continuación presentamos reunidos estos principios a modo de recapitulación.
1.- En el vacío absoluto no se puede producir ningún campo de fuerza, pues la única
propiedad que tiene el vacío es la de poder ser ocupado por la materia.
2.- El éter es el medio material en el cual se producen los campos de fuerza, la
propagación de las ondas electromagnéticas y las radiaciones fotónicas.
3.- La velocidad de la luz no es una magnitud constante, sino que es función inversa de
la densidad del éter.
4.- La fuerza coeléctrica producida en el contacto de una partícula con el éter es la causa
común de todas las fuerzas que se manifiestan a distancia, cualquiera que sea el tipo de
fuerza.
5.- Las cargas eléctricas de signo contrario, en contacto absoluto se atraen, mientras
que las del mismo signo no sufren ninguna fuerza de atracción ni tampoco de repulsión.
6.- El tiempo, el espacio, la masa gravitatoria y la carga eléctrica son magnitudes
absolutas y constantes.
7.- La velocidad, la cantidad de movimiento, la energía, la fuerza y la masa inercial son
magnitudes relativas.
8.- La masa inercial crece al aumentar la densidad del éter.
9.- La fuerza eléctrica y la magnética disminuyen al aumentar la velocidad de las cargas
eléctricas respecto al éter.
10.- El campo gravitatorio condiciona la mecánica de los astros mientras que el campo
gravitónico condiciona la de los átomos.
11.- La energía del campo eléctrico más la energía del campo magnético de una carga es
una cantidad constante cuando varía la velocidad de dicha carga.
12.- Todas las formas de energía distintas de la energía cinética son un estado latente de
esta última.
13.- Todas las partículas están constituidas por cargas eléctricas elementales.
14.- Todas las partículas tienen masa, incluso los neutrinos.
15.- La carga eléctrica neta de las partículas con carga se acumula en la superficie de las
mismas, en una capa única.
16.- Los electrones no son esféricos sino filiformes.
17.- La energía de los fotones está constituida por una mitad de energía cinética y otra
mitad de energía electromagnética.
18.- Las radiaciones fotónicas no son únicamente ondas electromagnéticas, sino que
transportan una cantidad de masa con ellas, mientras las ondas electromagnéticas puras
carecen de masa.
19.- La masa no se convierte en energía, sino que la energía es una condición relativa de
la masa.
20.- La masa, la carga eléctrica, la energía y la cantidad de movimiento, contenidos en un
sistema aislado, se mantienen constantes aunque se produzcan intercambios dentro del
sistema.
14.3. Nuevo interrogantes.
Como es habitual, al descubrir un nuevo horizonte, surgen nuevos interrogantes. En
nuestro caso, el lector habrá podido observar que hemos introducido en este trabajo
algunas magnitudes o coeficientes cuyo valor numérico ha quedado sin determinar. Son
los siguientes:
ρ
-
Densidad de nuestro éter ambiental.
Y
-
Factor de elasticidad del éter.
K1
-
Constante coeléctrica.
K2
-
Constante de densidad gravitatoria.
K3
-
Constante de densidad gravitónica.
K4
-
Relación entre la carga y la masa de los electrinos.
La determinación del valor numérico de estos factores constituye un desafío para la física
experimental, que no tardará mucho tiempo en superar.
Más lejana parece estar la respuesta para las siguientes preguntas: ¿por qué se asocian
las cargas eléctricas elementales de una manera determinada para constituir las
diferentes partículas subatómicas? ¿por qué unas partículas son estables y otras no lo
son?
Es razonable pensar que en otras regiones del universo, con diferente densidad del éter,
el comportamiento pudiera ser distinto y las partículas estables allí sean otras que las
conocidas por nosotros, mientras que nuestras partículas estables no lo sean allí.
Esta idea resulta reforzada si pensamos en las numerosas partículas de vida efímera que
se originan en los experimentos de desintegración nuclear. Estas partículas surgen en la
región de alta densidad del éter que rodea los núcleos, donde domina el campo
gravitónico, por lo tanto parece lógico pensar que se hacen inestables en el momento que
abandonan dicha región, lo cual explicaría lo efímero de su vida.
El autor es consciente de que esta tesis será rechazada por aquellos científicos que
tienen una fe ciega en la Relatividad Especial, más aún si se dejan influir por el austero
bagaje matemático con el que se presenta el trabajo. No obstante tiene la esperanza de
que pueda interesar a quien tenga una verdadera curiosidad por conocer las razones que
se ocultan detrás de los fenómenos físicos, sin valorar demasiado el rigor académico de la
presentación.
La implantación de la Teoría de la Relatividad Especial ha provocado el sentimiento de
que las causas primeras de los fenómenos físicos son algo incomprensible para la mente
humana y que debemos conformarnos con unos conceptos que no son razonables. De
aquí surge una tendencia a la especulación matemática sobre los principios establecidos,
renunciando a buscar una explicación razonada de los mismos.
Al haberse aceptado algunos postulados falsos, los resultados de esta especulación
conducen a verdaderos disparates, como espacios curvados o espacios con más de tres
dimensiones, así como a la idea de adjudicar a determinadas partículas la responsabilidad
de las distintas fuerzas, como sucede en el caso del “gravitón”, que es una partícula
inventada para explicar la fuerza gravitatoria, así como al fotón se le atribuyen las fuerzas
electromagnéticas, etc., en una especie de reparto de papeles que más parece un pasaje
mitológico que un asunto científico.
El conseguir una teoría unificada que relacionara entre sí los distintos campos de fuerza,
ha sido una aspiración obsesiva de algunos científicos, entre los cuales se encontraba
Einstein, pero el hecho de haber descartado el éter en sus planteamientos ha impedido
que sus esfuerzos tuvieran éxito, pues difícilmente se puede alcanzar una meta si se
empieza por eliminar el camino que conduce a la misma.